少なくともひとつが1になることの証明問題の解説他-高校数学の達人・河見賢司のメルマガ(2018年3月20日)
◇◆◇━━━━━━━━━━━━━━◇◆◇
高校数学の達人・河見賢司のメルマガ
◇◆◇━━━━━━━━━━━━━━◇◆◇
目次
【1】お知らせ
【2】数学の問題解説
数学IA 「6の倍数であることの証明」
数学IIB「x,y,zのうち少なくともともひとつが1になることの証明」
数学III 「無限等比級数の収束条件について」
【3】勉強法
「あえて悪問を解こう!」
【4】編集後記
【5】プロフィール
お知らせ
こんにちは、河見賢司です。
教えている生徒さんの結果発表があり、無事に神戸大学国際人間科学部に合格してくれました!!
最近の合格実績を振り返ってみました。ここ2年ほどは、新規の生徒さんの募集はしていません。だから、受験生は少なめです。
(コツコツとプリントを作っていました)
今年受験したのは2名で、一人が神戸大学でもう一人は推薦で工学院大学に行きました。
それ以前は、だいたい各学年6,7名ほど。ただ、なんとか高校を卒業するためとか、文系で数学は学校の授業だけでよい、という人多くいました。
だから、受験をする人自体は多くて5名。毎年、3名ほどでした。主な大学名を以下にあげています。
人数は少ないですが、合格率は圧倒的!!(自慢です)
(頑張ってくれた生徒さんは僕のほこりです。だから自慢します)
毎年、着実に大学に合格してくれているので、嬉しいです。
2018年
神戸大学国際人間科学部
2017年
島根大学医学部医学科
千葉大学国際教養学部
京都薬科大学薬学部
2016年
弘前大学医学部医学科
愛媛大学医学部医学科
京都大学工学部
2015年
東北大学歯学部
信州大学教育学部
2014年
関西医科大学医学科
中央大学法学部
筑波大学理工学群
2013年
防衛医科大学医学科
岡山大学医学部医学科
東京理科大学理工学部
いずれも進学した大学名を書いています。併願などで他大学にもかなり受かっています。
もちろん、すべて事実です。詳しくは以下のページを見てください。他にもいろいろな人がいます。
生徒様の声
昔のことを思い出してみると、当時授業を受けてくれた生徒さんの表情が思い浮かびます。これだけ多くの人が、一緒に頑張ってくれたんだな、と思えば嬉しくなります。
こうは言っては失礼ですけど、僕のところにくる人は数学に困り切った人がほとんどです。
これまで、宣伝もしたことないですし、存在するのは自作のこの怪しいホームページだけ。だから、数学に困り切った人しかきません。
でも、みなさん一生懸命頑張ってくれました。一生懸命頑張ったら、元の成績がどうであれ、結果が伴うのですね。
今年、神戸大学に合格をした生徒さんは、非常に頑張ってくれました。宿題も、毎回してくれました。
こういうふうに、「ホントに頑張ったな」と思える生徒さんの合格率は、100パーセント。記憶のある限り全員合格しています。
神様なんて言葉きらいな人がいます。でも、こうなったら神様はいる、頑張ったら絶対に神様が見てくれている、そう思えて仕方がないです。
前置きが長くなりました。それでは、今回もメルマガよろしくお願いします。
数学の問題解説
典型的な有名問題を中心に解説しています。「なぜ、そのように考えたのか?」ということを丁寧に説明しているので分かりやすいと思いますよ。
分かりやすいように、問題をレベル分けしています。問題を解くときの参考にしてください。
*難易度は、「基礎」「標準」「発展」「難問」に分けています。
「基礎」は教科書基本レベル。「標準」は定期試験向け、入試の基本問題。「発展」は国公立大学、MARCH、関関同立の志望者向け。「難問」は難関大学(上位国立、早慶、理科大)の志望者向け。
数学IA
「6の倍数であることの証明問題」
単元:「整数」 難易度:「基礎」
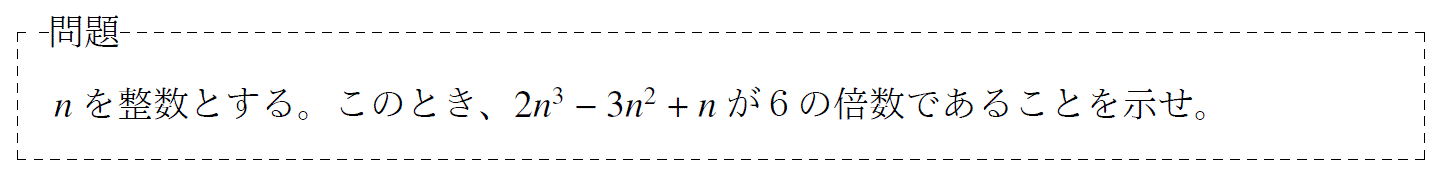
6の倍数であることの証明問題を解説しました。
「連続する3個の整数の積は6の倍数である」ことを使って示していきます。
詳しくは解説プリントを見て欲しいのですが、この事実を作るためにやや強引に式変形をします。
数学って、こういった強引な式変形をすることが多いです。
これは知っておかないと、なかなか思いつかないです。ぜひとも覚えておくようにしてください。
数学IIB
「x,y,zのうち少なくともひとつは1であることを示す証明問題」
単元:「式と証明」 難易度:「基礎」

「x,y,zのうち少なくともひとつは1であることを示せ」という問題を解説しました。
この問題は、「(x-1)(y-1)(z-1)=0」を示せばOKです。
これも覚えておかないとその場で思いつくのは難しいと思いますよ。
また、対称式の知識も必要になります。対称式をあまり理解出来ていないという人は以下のプリントで勉強をしてください。
対称式の解説プリント
対称式の練習問題の解説プリント
問題の考え方などは、プリントで解説しています。頑張ってください。
数学III
「無限等比級数の解説プリント」
単元:「極限」 難易度:「基礎」

無限等比級数について解説しました。無限等比級数は、数学Bの数列で勉強をした、等比数列の和の公式を覚えていれば簡単に理解することができます。
ごくごく簡単なところですが、こういったところをしっかりと理解できている人は少ないです。
プリントで詳しく解説しています。ぜひとも理解しておいてください。
数学の勉強法
「あえて、悪問を解いてみる」
今回のテーマは、「あえて悪問を解いてみる」です。
市販の問題集に掲載されている問題や塾・予備校のテキストに掲載されている問題は、いわゆる「良問」ばかりです。
ですが、実際の大学受験では「えっ!なんでこんな変わった問題を出すの?」とか「誘導問題が出てるけど、かえってまわりくどい解き方をしないとダメ」といったいわゆる悪問と言われるものも多く出題されます。
問題集に掲載されているようなストレートな問題ばかりを解いていると、そういったイレギュラーな問題に対応することができなくなってしまいます。
ですから、僕のところでは一通り勉強した後に、あえてイレギュラーな問題を問題を解いてもらうことがあります。
イレギュラーといっても、僕がテキトウに受験問題を選んだものです。
問題集でよく出てくるような典型問題もあれば、先ほどいった汚い問題もあります。そして、難易度もあえてバラバラにしています。
そういう問題を、解いてもらうことによって実践的な力が養われてきます。
受験数学って、きれいな問題ばかりが出題される訳ではありません。それらに対応できる力を養っておいてくださいね。
PS
こういうことを言うと、「何がきれいな問題で、何が汚い問題か判断できません」という人がいます。
確かにそうですよね。
で、僕のおすすめとしては志望校と似通った大学の過去問をテキトウに選んで問い見ることをおすすめします。
全部解くのがメンドウなら、例えば偶数番目の問題だけ、とかアトランダムに選んだらいいですよ。
「えっ、そんなテキトウな方法でいいの?」と思えるかもしれません。
でも、アトランダムの方がいいんです。自分で選ぶとどうしても、「この問題はしなくていい」などと自分の都合のよい方に解釈をしてしまいますから・・・
こんな勉強法、あまり言ってる人はいません。でも、ホントにお勧めですよ。
僕のところで難関大学に合格した人は、ほとんどの人にやってもらっています。ただ、これは一通り解法が身についたということが前提ですよ。
まったく、数学ができない段階で、これをやっても効果はありません。むしろ、逆効果です。
それでは、がんばってください。
編集後記
生徒さんが、神戸大学に合格してくれました。
僕、神戸で産まれて小学1年生の途中まで神戸で住んでいました。神戸といっても垂水区というところで、神戸の西端。
明石焼きで有名な明石のとなりです。
東舞子小学校というところにいて、とにかく生徒数が多かった。1,700人くらいいたかな?
垂水区と東隣りの須磨区の間は山と海が隣接しています。といいますか、山がほぼ海まできています。
その区間は、国道2号、JR、山陽電車が並走しています。
そこの景色が好きです。
電車も車も多く、そこそこ都会。登り、下りあわせたら1、2分おきに何かしらの電車が通過します。
すぐそこの海は瀬戸内海。瀬戸内海は、波もなく、おだやかそのもの。
のどかな漁船もあれば、タンカーなどの大型船もよく通る。
そして、明石海峡大橋。海の向こうには淡路島。
都会と田舎が混在している。
神戸方面の旅行で、わざわざ垂水や須磨に行く人は少ないと思います。
でも、もし機会があれば、のんびりと国道2号を垂水区と須磨区の間を走ってください。
楽しいと思いますよ。
河見賢司
河見のプロフィール
河見って、どんな人?と思った人は以下のプロフィールをみてください。
自宅に居ながらにして1対1の個別授業が受けられます
個別指導詳細
ルールを覚えれば誰でもできる!あなたの偏差値を70にするプリント
偏差値を70にするプリント
1時間からピンポイントで1対1の授業を受けられます。
ピンポイントの個別指導詳細
大好評の無料メルマガ。登録はコチラから
高校数学の達人・河見賢司のメルマガ
数学3の極限のプリントを無料でプレゼントします
数学3の極限の無料プリントを作りました。全部51問186ページの大作です。
このプリントをするだけで、学校の定期試験で満点を取ることができます。完全無料、もちろん売り込みもしません。読まないと損ですよ。
以下の緑のボタンをクリックしてください。
3年間大手予備校に行ってもセンターすら6割ほどの浪人生が、4浪目に入会。そして、入会わずか9か月後に島根大学医学部医学科合格!
数学の成績が限りなく下位の高校生が、現役で筑波大学理工学群合格!
教科書の問題は解けるけど、難しくなるとどう考えてよいのか分からない人が、東北大学歯学部合格!
その秘訣は、プリントを読んでもらえば分かります。
以下の緑のボタンをクリックしてください。


