対称式を含んだ2変数関数の最大値・最小値問題を解説しました
こんにちは、河見賢司です。今回は、「対称式を含んだ2変数関数の最大値・最小値の問題」を解説します。
突然、「対称式を含んだ2変数関数の最大値・最小値の問題」と言われても分からないと思います。具体的には以下のような問題です。
\(x,y\)を実数とする、\(x^2+xy+y^2=1\)のとき\(xy+2\,(x+y)\)の最大値と最小値を求めよ。
上記のような問題は、特に難関大学で頻出ですが、学校では勉強をするところは少なく理解できている人は少ないと思います。
「文字消去するときは、範囲に注意する」ということを常に頭に入れておかないといけません。この問題でもこの考えが重要になります。
このプリントを読んで「当たり前の内容だな」と感じた人は十分数学の実力があります。「知らなかった」という人は少し勉強不足です。学校ではあまり勉強しない内容なので、知らない人も多いと思いますが数学の基礎となるところなのでしっかりと理解しておいてください。
対称式を含んだ2変数関数の最大値・最小値問題の解説
動画で解説しました。(16分43秒)
スマホでは見にくいかもしれません。スマホを縦向きではなく横向きで見た方が見やすいと思います。
\(x,y\)を実数とする、\(x^2+xy+y^2=1\)のとき\(xy+2\,(x+y)\)の最大値と最小値を求めよ。
上記のような問題です。この類の問題は、難しくはないんですけど知らないという人が多いです。という僕も高校生のときはしっかりと理解出来ている訳ではなく、なんとなくテキトウに解いていました。
でも、大学受験には頻出で、パッと思いつく範囲で、2005年の東工大で出題されています。
この問題は、簡単な大学では出題される可能性は低いですが、ある程度以上のレベルの大学ではよく出題されます。
有名なんですけど、なぜか学校では勉強をしないということが多いです。簡単な問題ですのでしっかりと理解しておくようにしてください。
この問題はどうやって解いていくかと言うと、\(x^2+xy+y^2\) も\(xy+2(x + y)\) も対称式なので \(x + y = u, xy = v\) とでも置き換えて解いていきます。
*「どうして\(x+y=u\),\(xy=v\)っておいたの?」なんて思う人もいます。でも、対称式の問題ではこういうふうに\(x+y=u,xy=v\)とおくことが多いです。別に他の文字でもいいけど、こういうふうにおくということを覚えておいてもらえばいいと思います。
\(x + y = u, xy = v\) と置き換えると \(x^2 + xy + y^2 = (x + y)^2 − xy = u^2 − v = 1\) となります。さらに \(xy + 2 (x + y) = v + 2u\) となるので、今回の問題は、「\(u^2 − 2v = 1\) のとき \(v + 2u\) の最大値と最小値を求めたらいいのかな?」と思います。
確かにこういうふうに解いていくのですが、少し忘れてはいけないことがあります。
それは文字消去するときの注意点です。文字を消去するときは必ず範囲について考えないといけません。このあたりのことが分からない人は
https://www.hmg-gen.com/h-mojisyoukyo.pdf
を見てください。
今回の問題では \(x, y\) を消去して \(u, v\) のみの式にしてから考えていきます。文字消去するときは、範囲に注意するという考えに従うと、\(x, y\) を消去するときは当然 \(u, v\) がどのような範囲をとりうるか考える必要があります。
今から、\(x, y\) が実数全体を動くときの \(u, v\) の値の範囲がどうなるか考えないとダメなんだけど、\(u, v\) の値の範囲の求め方わかるかな?
解と係数の関係を使うと \(x, y\) を2解とするような2次方程式は \(X^2 − u X + v = 0\) だよね?
\(x, y\) は実数なんだから、実数 \(x, y\) が存在するための条件はこの方程式が実数解をもつ条件と同じ (\(x, y\) はこの方程式の解。\(x, y\) は実数なんだから、当然方程式は実数解をもたないといけない)、この方程式の判別式を \(D\) とすると、実数 \(x, y\) が存在するには \(D \geq0\) のときとなります。
(注) たまに\( x, y\) 2つの実数が存在するのだから\(D > 0\) じゃないか?と質問をする人がいますが、今回は \(x \neq y \)という条件が与えられていないので \(x = y\) のときもOKです。つまり \(D = 0\) のときも大丈夫です
\(D = u^2 − 4v \geq0 \)となるので、\(x + y = u, xy = v\) の式を使って実数 \(x, y\) を消去して \(u, v\) のみの式にするときは \(u^2 − 4v \geq0\) という条件が付いてきます。
はじめて見る人は少しややこしいかもしれませんが、本当に典型的な問題でよく出題されます。しっかりと理解しておいてください。それでは、解答に進みます。少し間が空いたのでもう一度問題を書いておきます。
\(x,y\)を実数とする、\(x^2+xy+y^2=1\)のとき\(xy+2\,(x+y)\)の最大値と最小値を求めよ。
【解答】
\(x+y=u,xy=v\)とする。
\(x,y\)は実数なので、\(X\)の2次方程式\(X^2-uX+v=0\)が実数解をもつ。この方程式の判別式を\(D\)とすると\(D=u^2-4v\geq0\)である。
\(\begin{aligned}
x^2+xy+y^2&=1\\
(x+y)^2-xy&=1\\
u^2-v&=1
\end{aligned}\)
\(xy+2\,(x+y)=v+2u\)
以上より、求める最大値と最小値は\(u^2-4v\geq0,u^2-y=1\)のときの、\(v+2u\)の最大値と最小値と一致する。以下、これの最大値と最小値を求める。
\(\begin{aligned}
u^2-4v&\geq0\\
u^2-4\,(u^2-1)&\geq0
\;{\color{red}{\Leftarrow \text{\(8v=u^2-1\)を代入した!}}}\\
-3u^2+4&\geq0\\
3u^2-4&\leq0\\
(\sqrt{3}u-2)(\sqrt{3}u+2)&\leq0\\
-\frac{2}{\sqrt{3}}\leq u&\leq\frac{2}{\sqrt{3}}
\;{\color{red}{\Leftarrow \text{\(v\)を消去したときの\(u\)の範囲が求まった!}}}
\end{aligned}\)
\begin{aligned}
&v+2u\\
=&u^2-1+2u
\;{\color{red}{\Leftarrow \text{\(v=2u^2-1\)を代入した!}}}\\
=&(u+1)^2-2
\end{aligned}
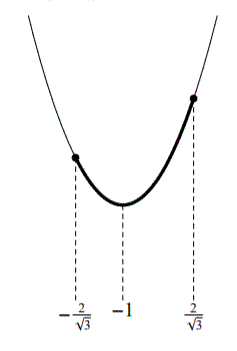
グラフより、\(u=-1\)のとき最小値-2をとり、
\(u=\frac{2}{\sqrt{3}}\)のとき最大値\(\frac{4}{3}\sqrt{3}+\frac{1}{3}\)をとる。
今回の問題解説はこれで終わりです。この対称式を含んだ2変数関数の最大値・最小値問題はよく出題されます。しっかりと理解しておいてください。
数学3の極限のプリントを無料でプレゼントします
数学3の極限の無料プリントを作りました。全部51問186ページの大作です。
このプリントをするだけで、学校の定期試験で満点を取ることができます。完全無料、もちろん売り込みもしません。読まないと損ですよ。
以下の緑のボタンをクリックしてください。
3年間大手予備校に行ってもセンターすら6割ほどの浪人生が、4浪目に入会。そして、入会わずか9か月後に島根大学医学部医学科合格!
数学の成績が限りなく下位の高校生が、現役で筑波大学理工学群合格!
教科書の問題は解けるけど、難しくなるとどう考えてよいのか分からない人が、東北大学歯学部合格!
その秘訣は、プリントを読んでもらえば分かります。
以下の緑のボタンをクリックしてください。


