分母に変数があるときの最大値・最小値の問題を2通りの方法で解説しました
問題
$$\text{\(x>0\)のとき、関数\(\frac{x}{x^2+x+1}\)の最大値を求めよ。}$$
【注意】
かなりの長文です。1回ではなかなか理解できません。2回、3回と繰り返し読めば言わんとしていることが分かってくると思います。
少しでも「ああ、なんとなく言っていること分かる!!」と思えるのでしたら、繰り返し繰り返し読んでください。そうすれば、あなたの数学の実力が各段に上がりますよ。
相加相乗平均を使って解く解法
 河見
河見はい、じゃあ今日は上記の問題を解いてもらうね。どう解くか分かる?

関数の最大値・最小値は確かグラフを描いて解くのだからグラフを描いて解いていけばいいのかな?
 河見
河見そう、そう関数の最大値・最小値はグラフを使って解いていくことが多いんだったんだよね。でも、今回の問題は\(\frac{x}{x^2+x+1}\)と分数に変数を含んだ関数です。
こういうふうに分数に変数を含んだ関数は数学3を勉強しないと描けないよ。それに、数学3を勉強していたとして、単純にグラフを描いて解く問題はあまり出題されないんだ

どうしてですか?
 河見
河見別に数学的な根拠があるから言っている訳じゃないです。実際今回の問題も\(y=\frac{x}{x^2+x+1}\)としてグラフを描くこともできるよ。だから、グラフを描いて解いていく方法も正解です。
でも、でもね、このグラフを描くっていう方法だったら数学3を勉強した人ならほぼ全員出来るんだ。単に計算が大変なだけ。大学側は「単に計算するだけの問題」はあまり出題しないんだ。
数学の試験は大学側が受験生の数学の能力を知りたくて出題している。でも、計算だけで誰でも解けるような問題あまり出題しないよね。この考え方絶対ではないよ。単にメンドウなだけの計算問題を出してくる大学もあるし・・・ただ、頭の片隅にでも入れておいてもらえれば、役に立つと思うよ。

分かりました。じゃあ、どうしようかな?確か、この前「分母に変数がある関数の最大値・最小値問題は相加相乗平均を使って解くことが多い」と言ってませんでした?
 河見
河見そう正解!!この問題は相加相乗平均を使って解いていくよ。
問題に進むその前に「分母に変数が含まれている関数の最大値・最小値問題は相加相乗平均を使うことが多い」ってよく覚えていたね。こういうふうに、覚えるべきことをひとつずつ覚えていけば必ずできるようになるよ。
この調子で頑張ってね

ありがとうございます。頑張ります。今まで「どうしてそんなことするのかな?」と思っていたけど、言葉で覚えていけば簡単です。あっ、でも簡単なんて言ったら数学の神様に怒られるかも???
 河見
河見ちょっと、ゴメンね。数学の神様って・・・。そういうこと言う人なんだか多い。でも、関係ない「オレが神だっ!!」って感じでやっていたら数学の神様もひれ伏せてくれるよ。訳わからんこと言って、ごめん。

なんだか、先生らしい。僕もその気合で頑張ります(笑)
 河見
河見あまり「オレが神だ!」のこと言わないでね。なんとなく、テンションで言ってみただけだから・・・たまに、というかしょっちゅう変なこと言うけど、無視しててね。
じゃあ、問題に戻ります。今回の問題は、相加相乗平均を使うんだよね。で、今回の問題はまず\(\frac{x}{x^2+x+1}\)の分母分子を\(x\)で割ります。
よく、「なんで\(x\)で割るの?」と聞かれるけど、「そんなものだ」と思っていいですよ。「こういうふうにしたらうまくいきます」と考えてください。
とりあえずの根拠としては、分母と分子を\(x\)で割ったら、変数の\(x\)が含まれているのは分母だけで、分子は\(x\)がなくなって定数です。
こういうふうに、分母または分子が定数。あっ、でも分子が定数のときが圧倒的に多いかな?分子の変数をなくして、分母にのみ変数が含まれる形にしたらうまくいくことが多いです。
変数を含んでいるのは分母だけ。ということは、分子はとりあえずほっておいて、分母だけで考えていくことができるからです。
まあ、理屈をこねればこんな感じなんだけど、これは有名な問題だから解法を覚えておいてね。

はい、わかりました。数学って、覚えるところは覚えると割り切って覚えていった方がいいんですよね?
 河見
河見そうそう、割り切って覚えてください。
僕も理屈っぽくて、だから一生懸命考えていたんです。でも、一向にできるようにならない。そんなとき、思い切って割り切ってどんどんと進めていった。それで、あるとき気が付いたら急にできるようになっていた
もちろん、理詰めで考えたい人はそれでいいですよ。ただ、成績が上がらくて困っている人はやっぱり勉強の仕方が間違っているんだから、何かしら勉強の仕方を変えた方がいいよ。

僕も、割り切って進めることにしました。なんだか、理詰めてやっていった方がいいような気もするけど、僕には無理っぽいということが感じてきたから・・・
 河見
河見じゃあ、それで頑張っていってね。大丈夫、どんな方法でも必ずできるようになるよ。
じゃあ、今回の問題に戻るね。\(\frac{x}{x^2+x+1}\)の分母分子を\(x\)で割るね。そうすると、\(\frac{1}{x+1+\frac{1}{x}}\)となります。あっ、後言い忘れていたけど変数で割るときは0になるかどうか必ず注意してね。
数学では、0で割るということは絶対にしたらダメですよ。今回の場合、\(x>0\)で考えています。つまり、\(x=0\)となることはないので、分母分子を\(x\)で割ってOKです。

ここまできたら簡単だ。分かります。分母の\(x+\frac{1}{x}\)は相加相乗平均より\(x+\frac{1}{x}\geq2\sqrt{x\cdot\frac{1}{x}}=2\)だから、
\(x+1+\frac{1}{x}\geq3\)
今回分子は1の定数で、分母は3以上。分母分子ともに正で分子が定数のときは、分母の値が大きくなればなるほど分数全体の値としては逆に小さくなる。
\(x+1+\frac{1}{x}\geq3\)だから\(\frac{1}{x+1+\frac{1}{x}}\leq3\)となる。だから、今回の分数\(\frac{1}{x+1+\frac{1}{x}}\)の最大値は\(\frac{1}{3}\)となります!!
(*\(\geq\)は大なりイコール(以上)のことです。日本ではイコールを書きますが、海外では1本線とのことです。)
 河見
河見そうそう答えとしてはあっているけど、ちょっとその答え方じゃ減点されちゃうよ。どこが、減点対象か分かる?

どこかな?分母が最小のとき分母が最大になるというくだりはあっていると思うし・・・どこかな??
 河見
河見結論から言えば、等号成立条件を言っていないからだよ
例えば、\(f(x)\leq2\)のとき、\(f(x)\)の最大値は2と言えるかな?

言えるような、言えないような。よく分かりません。
 河見
河見いやらしい聞き方してゴメンね。\(f(x)\leq2\)だけでは\(f(x)\)の最大値が2とは確定しないんだ。
\(f(x)\leq2\)とは(\(f(x)<2\,\,\text{または}\,\,f(x)=2\))ということです。数学における「または」はどちらか一方でも満たしていればOKです。だから、例えば\(f(x)\)の最大値が1だったとしても、\(f(x)\leq2\)を満たしているよね。だから、\(f(x)\leq2\)からだけでは、\(f(x)\)の最大値が2であるということは言えないよ

確かにそうです。でも、ややこしい・・・
 河見
河見で、もし\(f(x)\leq2\)かつ\(f(x)=2\)となる\(x\)が存在したとしたら、\(f(x)\)の最大値は2であるということが言えるよね。
だから、「不等式で最大値・最小値問題を解くときは、等号成立条件を必ず書く」ということを覚えておいてね。
ホントは上記の日本語少しおかしいんだ。なぜかというと、「等号が成立することが前提」になっているからです。等号成立するかどうかわからないのに、そんなのおかしいよね。
でも、実際の大学受験の問題で、例えば「\(f(x)\leq2\)」が出てきて、\(f(x)\)の最大値が2でない、問題なんか見たことないんです。だから、「\(f(x)\leq2\)」を見た瞬間に最大値が2だと思ってもまず間違いないですよ。
ただ、そのときでも等号成立する\(x\)が存在するということを書いておかないと大幅に減点されるから気を付けてくださいね。ホントは、こんな考え方ダメかもしれないんだけど、まあ「大学受験で点数をとる」ということに割り切ったら、これでもいいと思うよ。もし、もっと丁寧に勉強したいなら大学に入ってから勉強してね。
大学に受からなければ、大学の勉強をしたいと思っても無理なんだから、高校生のうちは割り切って合格することだけを考えた方がいいと思うよ。

僕は、とりあえず大学に受かればOKなので、そんな細かいことは考えないことにします・・・
 河見
河見実は、僕も「受かればOK」の考え!でも、数学講師と名乗っているからあまり大きな声では言えない・・・

河見先生のそういったところ好きです。なんだか、他の数学の先生はかたっ苦しい・・・
 河見
河見ありがとね。でも、他の数学の先生が言っていることもよく分かる。僕なんか「受かったらいいやん!」みたいな感じでやっていた。でも、やっぱり丁寧に数学をひとつずつ理解していくことも重要。
ただ、高校生でそこまでできる人ってほんのわずかだと思うんです。だから、ホントはダメかもしれないけど、まずは受験数学で点数を取ることに割り切って、そして大学に入ってから勉強したい人は勉強したらいいと思います。
ごめん、話しが大きくそれちゃった。問題に戻るね。今回の問題は、あとは等号成立条件を言っておけばOKです。詳しくは、動画で解説してるから、動画を見てください。
 河見
河見ごめん、動画って一人で話しているからどうもペースが作れなくて・・・早口になったり活舌が悪くなったりしているかも?まあ、僕が言わんとしていることはわかると思います。
今回の問題は、相加相乗平均を使って解くのが一番ラクです。ただ、逆手流や逆像法と呼ばれる解法で解くこともできます。グラフの考え方など重要です。少しややこしい解き方ですが、あえて解いてみることにしました。
逆手流・逆像法を使って解く解法
 河見
河見今回の問題なんだけど、さっき解いたように相加相乗平均で解くのが一番おすすめです。でも、逆手流や逆像法と呼ばれる解法で解くこともできます。

逆手流とか逆像法とか、なんとなく聞いたことがあります。
 河見
河見逆手流とか逆像法は数学の言葉というより、とある予備校や問題集で使われていた言葉です。だから、言葉自体は別に覚えなくていいよ。でも、この逆手流・逆像法は重要だから話しておくことにするね。
突然だけど、「\(x^2+y^2=1\)のとき、\(x+y\)の最大値と最小値を求めよ」という問題解けるかな?

はい、それだったら\(x+y=k\)とおいて、直線\(x+y=k\)と円\(x^2+y^2=1\)が共有点をもつときを求めて、\(-\sqrt{2}\leq k\leq\sqrt{2}\)となって、最小値は\(-\sqrt{2}\)で最大値は\(\sqrt{2}\)です。
 河見
河見そう、答えとしてそれであっているよ。でも、「なんで\(x+y=k\)と置いたの?」「なんで直線と円が共有点をもつの?」ってなったら答えられない人が多いよね。

確かにそうだ。僕も、この問題のときは「こう解くものだ」といった感じで答えていました。ちゃんと説明しなさい、と言われても説明できません。
 河見
河見そうだよね。大多数の高校生がそうだと思うよ。偉そうに言っている僕も高校生のときは、意味も分からずに解いていました。
簡単な問題だったら、それでいいんだけど、難しくなったらそれでは解けなくなってしまいます。さっき、「\(x+y=k\)とおいて・・・」と言ったよね。これが、逆手流・逆像法の解法なんだ。

??
 河見
河見意味わかんないよね。だから、逆手流・逆像法について今から詳しく話していきます。
さっきの問題を例にとって話していくことにするね。

はい、お願いします。
 河見
河見「\(x^2+y^2=1\)のとき、\(x+y\)の最大値・最小値を求めよ」なんだけど「\(x+y\)」の最大値・最小値なんだよね。ということは、\(x\)と\(y\)の2変数関数です。
2変数関数の最大値・最小値問題では1変数にしてから解いていくことが多かったんだよね。だから、今回も「\(x+y\)」を1変数にしたいんだけど、これはできそうにないよね・・・
厳密に言えば、\(x^2+y^2=1\)を\(y\)で解けば、\(y=\pm\sqrt{1-x^2}\)だからこれより\(x+y=x\pm\sqrt{1-x^2}\)として\(x\)のみの1変数にできないことはないよ。
ただ、こんなことする訳ないよね。\(x\pm\sqrt{1-x^2}\)は複雑すぎて扱えません。そこで、別の解法を考えないといけないんだけど・・・そこで出てくるので逆手流・逆像法という解法です。今から、逆手流・逆像法について話していくことにするね。

分かりました。
 河見
河見突然なんだけど、\(x^2+y^2=1\)のとき、\(x+y=1\)となるかどうかわかる?

えっ?どうだろう?単純に\(x+y=1\)より\(y=x-1\)として、\(x^2+y^2=1\)に代入したら\(x\)と\(y\)が求められるんじゃないですか?
 河見
河見そうそうほとんどあっているよ。\(x+y=1\)となるかどうかなんだけど、もっと厳密に言えば、「\({x^2+y^2=1}\)かつ\({x+y=1}\)を満たす実数\({x,y}\)が存在したら、\({x+y=1}\)となることがある」となります。分かるかな?

なんとなく分かります。
 河見
河見そうそう最初のうちはなんとなくでいいよ。
これって逆から考えているから考えにくい。\(x^2+y^2=1\)かつ\(x+y=1\)となっているけど、この2式を連立して解くと\((x,y)=(0,1),(1,0)\)となります。
今回は「\(x^2+y^2=1\)のとき、\(x+y=1\)となるかどうか」を聞いていたんだよね。で、\((x,y)=(1,0),(0,1)\)のとき\(x^2+y^2=1\)を満たしていて、\(x+y=1\)となってくれるんだよね。
だから、「\(x^2+y^2=1\)のとき、\(x+y=1\)となるかどうか」の判断の仕方は、この2式を連立したときの実数解の組\(x,y\)が存在してくれるかどうかで判断できます。今回の場合、\((x,y)=(1,0),(0,1)\)と実数解の組をもったので、「\(x^2+y^2=1\)のとき、\(x+y=1\)となる」ということが分かりました。
回りくどい説明でごめんなさいね。もし、わからなけらば「こんなもんだ」と割り切ってやってもらったら大丈夫ですよ。逆手流・逆像法についていはこれから何度も出てくるので、テキトウにやっていてもそのうち理解できるようになるよ。

分かりました。
 河見
河見で、さっきは「\(x+y=1\)」と具体的な値で解いたけど、これを\(x+y=k\)とでもして解いていきます。\(x+y\)が\(k\)という値をとるとき、「\(x^2+y^2=1\)かつ\(x+y=k\)」が実数解の組を持てばいいんだよね。
で、ここから単純に\(x+y=k\)より\(y=k-x\)として、\(x^2+y^2=1\)に代入して整理すると、\(2x^2-2kx+k^2-1=0\)となります。連立方程式が実数解の組\(x,y\)をもつんだよね。このとき、実数\(x\)が存在しないとダメなんだから、さっきの\(x\)の2次方程式\(2x^2-2kx+k^2-1=0\)が実数解をもちます。
で、今は実数解の組\((x,y)\)がないとダメだったんだよね。でも、\(x+y=k\)とおいて\(k\)は実数です。\(y=k-x\)より、\(k\)は実数で\(x\)も実数だったら\(y\)も実数となるよね。
だから、さっきの\(x\)についての2次方程式が実数解をもてば実数\(y\)も存在してくれます。
先ほどの、2次方程式\(2x^2-2kx+k^2-1=0\)が実数解をもつとき\(D\geq0\)を解くと\(-\sqrt{2}\leq k\leq\sqrt{2}\)です。これより、\(-\sqrt{2}\)が最小値で\(\sqrt{2}\)が最大値となるよ。
あっ、それから不等式を使って最大値最小値を求めるときは、等号成立条件を考えておかないとダメなんだよね。今回の問題も等号を求めておいた方がいいと思います。
数学って、少し不思議なところがあって、今回のようなとき「等号が成立するような\(x,y\)が存在することは自明」と扱う人もいます。だから、今回の問題に関しては等号成立条件を書いていなくても減点されないこともあります。ただ、個人的に減点される可能性がある以上等号成立条件をかいておいた方がいいと思いますよ。

なんだか、ややこしいですね。まだ、少しもやっとしています。でも、復習頑張っておきます。
一番最初解いたとき、直線\(x+y=k\)と円\(x^2+y^2=1\)が共有点をもつといいました。でも、これって連立方程式が実数解の組をもつってことだんたんですね。確かに、連立方程式が実数解をもつとき、2曲線は共有点をもちますよね。
 河見
河見そうそう、「連立方程式\(x^2+y^2=1\,x+y=k\)が実数解の組をもつ」ことと「円\(x^2+y^2=1\)と直線\(x+y=k\)が共有点をもつこと」は同値ですよ。式で考えた方が簡単な場合もあるし、グラフの共有点で考えた方が簡単な場合もあります。どっちが簡単かは、その場その場で考えるようにしておいてくださいね。
こういうふうに、最大値や最小値を直接求めることができないときに、\(x+y=k\)とおいて解いていく解法を逆手流や逆像法といいます。よく出てくるので覚えておいてくださいね。前置きが長くなったけど、今回の問題に進むことにするね。

あっ、今回の問題まだだった。疲れました・・・今回の授業、たった1問なのにかなりハードです・・・
 河見
河見説明長くなってごめんね。ここまで話さないと理解できないよね。というか、これだけ話してもまだ理解しにくい部分もあると思う。できるだけ、理解しやすく解説しています。
でも、でもこれって普通の人は、一度で理解することはなかなか難しいよ。

そうなんですか?(なんとなく慰められているような・・・)
 河見
河見数学ってスポーツと同じだよね。あっ、たしかバスケ部だったよね。

あっ、バスケ部です。僕、スリーポイントシュートが結構得意です。
 河見
河見へースリーポイントできる人ってカッコいいよね。僕はたぶん10回シュートしても1回も入らない。自信がありますわ。
で、さっきの「数学とスポーツが同じ」なんだけど、例えばバスケの初心者がスリーポイントシュートの打ち方を人から聞きます。それですぐにうまくうてる?

いや無理。そりゃ練習しないとなかなか決まらない。
 河見
河見「スリーポイントの仕方習ったのに、なんで決まらないの?」なんて習った日に憤慨している人みたらどう思う?

・・・
 河見
河見僕の言わんとしていること分かるよね。スポーツだったらすぐに理解するけど、数学となれば理解できない人が多いみたい。「数学もスポーツと同じで、聞いてすぐにできるようにならないよ」

そうですか?でも、数学とスポーツは違うような・・・だって、同じクラスの頭のいい奴先生の言うことをすぐに理解出来ていますよ。
 河見
河見確かにそういう人もいるよね。でも、これってスポーツも同じ。運動神経のいい人いるよね。数学もそれと同じ。でもでもそんなこと、ひがんでも仕方がないよね。
だから、あきらめてやった方がいいよ。

数学が苦手な僕でもできるようになるのかな?
 河見
河見ちょっと、クサい話するね。恥ずかしいけど、一応話してみます。もし、「うさんくさい」と思ったら信じないでね。この人おかしなこと言ってるよ、と無視してください。
僕、小学生のころ野球が好きだった。でも、将来プロ野球選手になろうなんて考えなかった。

????
 河見
河見自分がプロ野球選手になる能力なんてまったくない、ということが自覚できていた。だから、プロ野球選手になろうなんてこれっぽっちも考えなかった。
小さい頃から僕は頭が悪かったけど、無謀にも難しい大学に行きたくなった。どうしても、やりたくなった。
結果として、志望校に受かることはできなかったけど、それでも自分は満足だった。「ああ。頭の悪い僕でも頑張ったらここまでたどりつくことができたんだ」と思うことができた。
作家の望月さんという人が「叶う夢だからあなたに宿る」ということを言っていました。
「何を言ってんだ」なんて思う人もいるかもしれないけど、僕はこの言葉、むちゃくちゃ腑に落ちた。ほんのちょっとの思い付きとかそういったものでなくて、例えば「どうしても医学部に行きたい」とか「この大学に行きたい」という人で、無謀なことを言っている人はいなかった。
将来お医者さんになりたいと思っても、もしその人に能力がなかったのなら医学部に行きたい、なんて思わない。「お医者さんてカッコいいけど、自分には無理。だから、他の進路を考えよう」と。かつての僕が野球選手になろうと思わなかったのと同じ事。
案外、人間は自分の能力を客観的に判断できているのかな?と思う。だから、もし行きたい大学がある、それが心の底からのものなら、何も遠慮することない。一生懸命頑張れば必ず結果がついてくる。
そうなったら他人の才能なんてどうでもよくなる。他人に嫉妬しているということは、「まだ自分の才能を出し切っていない」という自分からのメッセージだと思う。
数学に関係ないこと、語ってゴメンね。でも、僕数学を教えさせてもらっているけど、ホントに伝えたいのはこのことなんだ。

分かるような。分からないような。
地元が同じでちょっとだけ知っているだけの人なんですけど、5歳くらい上の人がいました。
その人、相撲部屋からスカウトがきたみたいで「俺は大関、横綱を目指すんだ・・・」と大相撲の世界に進みました。
でも、結局うまくいかず序二段?とにかく、全然上にいけなくて辞めてしまっています。
そういう人を見たら、「あまり大きなものを目指すのはどうかな?」とついつい思ってしまいます。
 河見
河見確かにそうだよね。その大相撲に進んだ知り合いがどう思っていたのか分かりません。でも、僕の場合、僕浪人して結局志望校に行けなかった。まあ、はっきり言えば、失敗組です。
落ちた後はショックでした。正直いうと大学に進学してからもしばらく落ち込んでいた。別に、大学に不満があった訳でもないし、大学生活に不満があった訳でもない。でも、「ああ、一生懸命頑張ったのに結局役に立たなかったのかな?」なんて落ち込むこともありました。
でも、今僕がこうして多くの生徒さんと接点を持って、その人の夢をかなえるお手伝いができている。こんなに嬉しいことはないんです。あのとき僕が浪人して一生懸命頑張るという経験がなければできなかったことです。
いろいろあったけど、でも「がんばってみて良かったな」と心底思えます。だから、うまくいくこともあるし、いかないこともあるかもしれない。でも、一生懸命やっていれば次につながる何かが見えてくる、そんな気がします。
なんだか、変なことばっかり言ってごめんね。ついつい、いろいろなことを思い出しちゃって・・・でも、「叶う夢だからあなたに宿る」は絶対あっている!と思えてなりません。だって、僕のところで一生懸命頑張った人ほとんど合格してくれていますから・・・
もちろん、一生懸命頑張ったのにうまくいかなかった人もいます。圧倒的に少数だけど、それでも1人か2人います。今は連絡とっていないからどうなったか分かりません。でも、時間が経てばきっと「あのとき自分が頑張ったおかげで・・・」と思える瞬間がきます。そう信じています。
そろそろ問題に戻るね。

あっ、そうでした。数学の問題解いていたんですよね。
あのーさっきの話し、よく分かったような、分からなかったような・・・
とりあえず、僕もあまり頭よくないけど、頑張ってみることにします。
 河見
河見うん、がんばってね。大丈夫、できるようになるよ。
それじゃあ、
\(\frac{x}{x^2+x+1}\)を逆手流・逆像法で解いていくね。
\(\frac{x}{x^2+x+1}=k\)をみたす正の実数\(x\)が存在、として解いていきます。分数だと考えにくいので、両辺に\(x^2+x+1\)をかけると、\(x=k(x^2+x+1)\)となり、整理すると\(kx^2+(k-1)x+k=0\)です。
\(k\neq0\)のとき、この\(kx^2+(k-1)x+k=0\)は2次方程式となるよね。もし、これが実数解をもつ条件だったら考えやすいんだけど、今回は「正の実数解」をもたないとダメ。
2次方程式が正の実数解をもつ問題って、結構ややこしいの覚えている?数学Iで勉強する内容だよ。

ああ、それ理解しています。解が2個とも正のときとか、1個が正で1個が負とか場合分けが必要な問題ですよね。
解けることは解けるけど、メンドウだったという記憶があります。
 河見
河見「\(kx^2+(k-1)x+k=0\)が正の実数解をもつ」と、「\(y=kx^2+(k-1)\,x+k\)のグラフと\(y=0\)のグラフつまり\(x\)軸が、\(x>0\)の部分で共有点をもつ」は同値なんだよね。
だから、これで解いていっても解けないことはないです。でも、別にこれにこだわる必要はない。例えば\(kx^2+(k-1)x+k=0\)で\((k-1)x\)を移項して、
\(kx^2+k=-(k-1)x\)として\(y=kx^2+k,y=-(k-1)x\)の2つのグラフで考えていってもOKです。

ああ、確かにそうですね。これまで2次方程式の問題だったら、何も考えずに放物線と\(x\)軸で考えていたけど、別に他のものでやってもいいんだ。
 河見
河見そうそう、ほとんどの問題集では放物線と\(x\)軸にこだわっているけど、別にこれで解く必要はないよ。
で、どういうふうに変形するかということなんだけど、できるだけ簡単な方がいいよね。

もちろんです。簡単にこしたことはないです。
 河見
河見今回\(k\neq0\)が言えているんだ。なぜかと言えば、\(kx^2+(k-1)x+k=0\)に\(k=0\)を代入してみれば、\(-x=0\)つまり\(x=0\)です。でも、今回、正の解をもたないといけないんだよね。0は正の数でないから不適です。だから、\(k\neq0\)が言えます。
なぜ、\(k\neq0\)の話をしたのかと言うと、\(k\)を分母にもってくるからです。分母にくるのは0だったらダメなんだよね。だから、確認しました。
今回\(\frac{x}{x^2+x+1}=k\)を変形して、\(\frac{1}{k}x=x^2+x+1\)となります。これで、直線\(y=\frac{1}{k}x\)と放物線\(y=x^2+x+1\)で考えていくことのします。

\(k\)が分母にきてなんだかややこしくなって気がします。どうして、そう変形したのですか?
 河見
河見そうそうそう、一見ややこしくなったよね。でも、これにはポイントがあります。今回定数の\(k\)は1次式につけました。別に、\(x=k(x^2+x+1)\)としても数学的に間違っている訳ではありません。これは、定数の\(k\)は2次式についているよね。
こういうふうに定数を含んだ方程式で2つに分けるとき、\(\underline{k=\cdots}\)のように定数分離をすることが多かったと思います。それ以外には定数は1次式につけることはあります。ですが、2次式以上で定数をつけることは少ないです。
別につけても数学的におかしいといいう訳ではないよ。だから、2次式以上につけても解けることもあります。ですが、一般的に2次式以上の場合、定数がかわったときのグラフがどうなるか?ということが認識しにくいんです。
一方で、例えば定数分離の\(k=\cdots\)の形なら、直線\(y=k\)で考えていけばいいんだよね。このとき、直線\(y=k\)は\(x\)軸に平行な直線なので考えやすいです。
それで、1次関数に\(k\)がついたらどうなの?と思うよね。でも、これって多くの場合、\(k\)の値に関係なく傾きが変わる直線になるから、考えやすいんです。ちょっと、話が長くなってややこしくなってきたよね。頑張ってついてきてね。

はい、頑張ります。
 河見
河見今回の、\(y=\frac{1}{k}x\)は原点を通る直線だよね。

はい、そうです。
 河見
河見そして、傾きは\(\frac{1}{k}\)なんだから、\(k\)の値が変わることで傾きが変わるだけです。
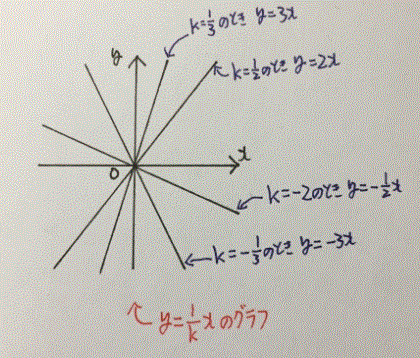
こういうふうに、直線に定数\(k\)の値が含まれていても単に傾きが変わるだけだから、グラフが把握しやすいんです。
「定数を含んでいいのは、定数項か1次式」ということを覚えておいてね。もちろん、例外はないとはいえないけど、あまり記憶にないです。だから、問題が出てきたら、とりあえず上記の考えでやってみたらいいと思うよ。それで、もしうまくいかなかったらその時点で考えるようにしてください。
これでやっと問題に戻れる。今回は、\(\frac{1}{k}x=x^2+x+1\)が正の実数解をもつような\(k\)の値の範囲を求めています。こうなるためには、直線\(y=\frac{1}{k}x\)と放物線\(y=x^2+x+1\)が正の部分で共有点をもてばOKです。
\(y=x^2+x+1\)\(=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)だから、図示すると以下のようになります。
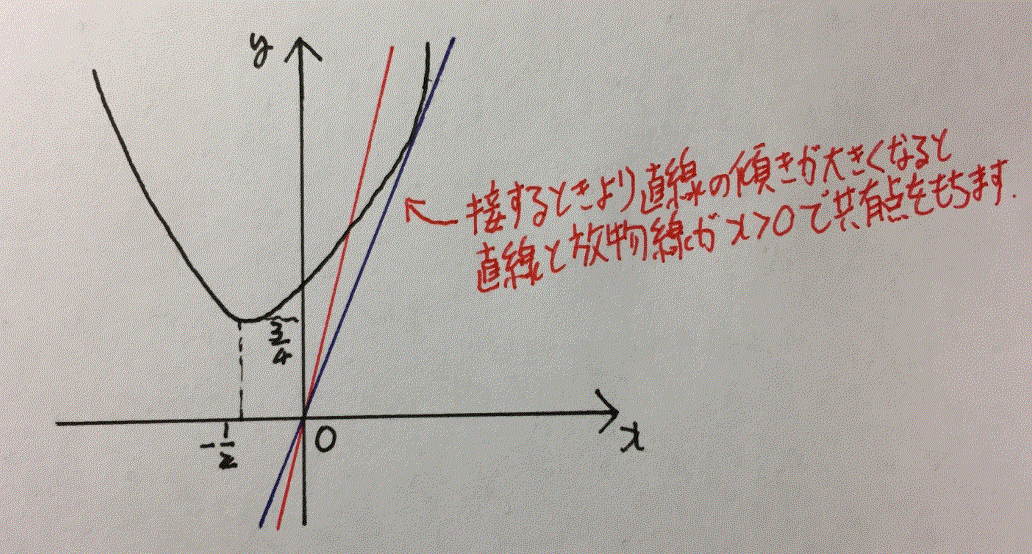
上図のように直線\(y=\frac{1}{k}x\)と放物線\(y=x^2+x+1\)が接するときがあって、それよりも直線の傾きが大きいときに直線と放物線が\(x>0\)の部分で共有点をもってくれるよね。
接するときは2次方程式の判別式から求めていけばOKだよね。2次方程式\(kx^2+(k-1)x+k=0\)の判別式を\(D\)として、\(D=0\)を解けば、\(k=-1,\frac{1}{3}\)となります。グラフより、当然傾きは正のときだから\(k=\frac{1}{3}\)となります。
\(k=\frac{1}{3}\)のとき傾きの\(\frac{1}{k}\)は3です。これよりも傾きが大きければよいので、\(\frac{1}{k}\geq3\)です。明らかに\(k>0\)なので、両辺に\(k\)をかけても不等号の向きは変わりません。不等式の両辺に文字式をかけるときは、必ずこのあたりのことを気を付けてくださいね。
不等式を解くと、\(k\leq\frac{1}{3}\)となるので、\(\frac{1}{3}\)が最大値です。不等式で最大値を求めたので、等号成立条件をかいておいてね。計算すると、\(x=1\)となってくれているよ。
フヒー、本当に長かった・・・でも、この問題覚えることが多くていろいろとためになることが多かったよね。頑張って理解しておいてくださいね。
数学3の極限のプリントを無料でプレゼントします
数学3の極限の無料プリントを作りました。全部51問186ページの大作です。
このプリントをするだけで、学校の定期試験で満点を取ることができます。完全無料、もちろん売り込みもしません。読まないと損ですよ。
以下の緑のボタンをクリックしてください。
3年間大手予備校に行ってもセンターすら6割ほどの浪人生が、4浪目に入会。そして、入会わずか9か月後に島根大学医学部医学科合格!
数学の成績が限りなく下位の高校生が、現役で筑波大学理工学群合格!
教科書の問題は解けるけど、難しくなるとどう考えてよいのか分からない人が、東北大学歯学部合格!
その秘訣は、プリントを読んでもらえば分かります。
以下の緑のボタンをクリックしてください。


