実際に高校生の人たちから質問を受けた箇所を説明していきます。まだまだ作りたでですが、徐々に充実させていきます。
質問と回答
目次
基本問題の解説プリント
基本問題と銘打っていますがプリントによっては難しい問題も扱っています。高校1年生や2年生の定期試験対策に最適ですよ。ぜひとも、利用してください。
漸化式
数列の漸化式の問題の解説プリントです。漸化式には、「このときは、こうやって解く」という決まりごと、ルールがあります。
そして、そのルールを覚えていけばワンパターンで解けてしまうので、簡単です。
よく「漸化式が難しい」という人がいますが、話しを聞いてみると単純に解法を覚えていないだけなんです。漸化式は解法を覚えておかないと絶対に解けるようにはなりませんよ。
このプリントでは、高校数学で覚えておかないといけない漸化式のすべてのパターンを網羅しています。漸化式に関してはこのプリントだけで大丈夫ですよ。
場合の数
本当に多くの人が苦手にしている場合の数を何度かにわたって解説します。
この場合の数のプリントは、特に場合の数の考え方を中心に解説しています。場合の数はなんとなく解いている人が多いと思います。
簡単な問題なら、それでも解くことができますが、難しくなると考え方そのものを理解していないと解けなくなってしまいます。
プリントに載せている問題はいずれも簡単なものです。ぜひとも場合の数が苦手だという人は、このプリントを使って勉強して下さい。
場合の数①「場合の数の考え方」
場合の数②「順列の考え方」
場合の数③「同じ文字を含む順列」と「組み合わせの公式」
場合の数④「最短経路」と「リンゴの配分に関する問題」
場合の数⑤「円順列」
場合の数⑥「組み分けに関する問題」
場合の数⑦「高校生から質問の多かった場合の数の問題」
2次関数
2次関数に関する問題を作成します。
高校数学において2次関数は関数分野の基礎となるところです。これから三角関数、指数対数、微分積分などの関数分野を勉強していきますが、2次関数を理解できているかそうでないかでこれらの単元の理解度がまってく違ってきます。
「三角関数が分からないんです」と言ってくる人が多いですが、三角関数が分からないという以前に2次関数が理解できていないということが多いです。
2次関数は、それくらい重要な単元ですのでしっかりと勉強して下さい。今回のこの2次関数のシリーズは解き方をしっかりと理解してもらうために、あえて基本的な問題が中心になっています。基本的ですが、手を抜かないでしっかりと勉強するようにしてください。
2次関数①「対称移動」
2次関数②「平行移動」
2次関数③「2次関数の決定」
2次関数④「2次関数がx軸によって切り取られる線分の長さに関する問題」
2次関数⑤「判別式について」
2次関数⑥「最大値、最小値の考え方」
2次関数⑦「場合分けの必要な最大値、最小値問題」
2次関数⑧「場合分けの必要な最大値、最小値問題 その2」
2次関数⑨「解の配置に関する問題」
数列のシグマの問題
数列のシグマに関する問題を作成しました。
シグマは、単元としては数列ですが、数学Ⅲで必要になるので、理系の人は数学Ⅲの勉強をする前にしっかりと理解しておかないといけません。やってもらえば分かると思いますが、決して難しい単元ではありません。このプリントを使ってしっかりと勉強しておいてください。
シグマの計算①「公式を使ったシグマの計算」
シグマの計算②「互いに打ち消しあうシグマの計算」
シグマの計算③「シグマの等差かける等比型」
数学の鉄則
数学の鉄則シリーズです。数学の鉄則とは、高校数学の問題のどの単元でも必要な考え方です。
文字消去や文字消去うするときの注意点を扱っています。内容としては本当に基礎的なものかもしれませんが、普段生徒に教えていてこのあたりを理解できていない人が本当に多いです。
全4回で内容的にも簡単なものです。しっかりと解いておいてください。
数学の鉄則①「文字消去」
数学の鉄則②「文字消去するときの注意点」
数学の鉄則③「文字を置き換えるときの注意点」
数学の鉄則④「不等式の両辺に変数をかけるときの注意点」
因数分解
因数分解です。全5回です。因数分解は解き方はワンパターンなので、いったん理解したら簡単に解けます。
因数分解は、大きく分けて5通りの解き方があります。その5通りすべて解説しています。ひとつずつ解き方
を覚えていってください。
因数分解①「公式を使った因数分解」
因数分解②「共通因数でくくりだす」
因数分解③「最低次が1次のときの因数分解」
因数分解④「最低次が2次のときの因数分解」
因数分解⑤「2乗マイナス2乗の因数分解」
対称式
対称式の問題です。対称式は、多くの教科書や問題集でもサラッと書かれているだけのことが多く、何気なく理解している人がほとんどです。でも、対称式の式変形は本当に重要なものです。
この対称式の式変形を何となく理解しているか、しっかりと理解できているかで今後難しい問題で、対称式の知識が必要なものにあたったときの理解度がまったく違うものになってきます。問題量がやや多く大変ですが、しっかりと理解しておいてください。
三角関数
三角関数の方程式は単位円を使って解く人が多いと思います。簡単なものなら単位円でも良いですが、少し複雑なものになると三角関数のグラフを使って解く方が考えやすいです。
三角関数のグラフは対称性さえ理解すれば本当に使いやすいです。短時間で理解できるものなのでしっかりと理解しておいてください。
グラフを使って解く、三角関数の方程式
(容量が5.5MBあります。注意してください。)
三角関数でsin(90-x)=cosxなどの公式があります。これらを暗記したり、図形からわざわざ導いている人もいますが、加法定理で導く方法が一番簡単だと思います。プリントに簡単にまとめておいたので、知らないという人は見てください。
加法定理を使ったsin(90-x)=cosxの導き方をアップしました
三角関数の問題です。三角関数は問題によって解き方が決まっています。ですから三角関数は典型問題の解き方を覚えたら、確実に解けるようになるます。
このプリントは、基本的な問題ばかりを紹介していきます。ただ、難関大学で出題される三角関数の問題も、解き方は同じです。途中、場合分けが複雑であったりして少し難しくなるかもしれませんが、この三角関数のシリーズさえ理解できていたら困ることはありません。このシリーズは現在作成中ですが全部で15回前後になると予想しています。プリントができ次第アップしていくので、よろしくお願いします。
三角関数①「三角関数の公式の確認」
三角関数②「三角関数の積和の公式」
三角関数③「sin,cos,tanの値を求める問題」
三角関数④「三角関数の対称式に関する問題」
三角関数⑤「置き換えの必要な三角関数の方程式」
三角関数⑥「置き換えの必要な三角関数の最大最小問題No1」
三角関数⑦「置き換えの必要な三角関数の最大最小問題No2」
三角関数⑧「置き換えの必要な三角関数の最大最小問題No3」
三角関数⑨「置き換えの必要な三角関数の最大最小問題No4」
三角関数⑩「asin^2x+bsinxcosx+ccos^2xに関する問題」
三角関数⑪「円の媒介変数表示に関する問題」
三角関数⑫「円の媒介変数表示に関する問題 その2」
三角関数⑬「18度に関する問題」
三角関数⑭「三角関数の連立方程式に関する問題」
三角関数⑮「三角形の形状に関する問題」
三角関数⑯「三角関数の解の個数の問題、その他の問題」
高校生からの質問があった問題の解説と数学のちょっとしたポイントを解説しました
質問と回答に載せているプリントの中で、特に読んで欲しいというものを集めました。
数学I+II+B
解説プリント その1
数学の問題って、「こう解いたらできるけど面倒だな」と思えるときありますよね。そういうときには、何か他のうまい解法が存在することが多いです。学校や予備校ではあまり語られることがない内容ですが、重要ですよ。
問題解説
典型的な有名問題を中心に解説しています。「なぜ、そのように考えたのか?」ということを丁寧に説明しているので分かりやすいと思いますよ。
分かりやすいように、問題をレベル分けしています。問題を解くときの参考にしてください。
*難易度は、「基礎」「標準」「発展」「難問」に分けています。
「基礎」は教科書基本レベル。「標準」は定期試験向け、入試の基本問題。「発展」は国公立大学、MARCH、関関同立の志望者向け。「難問」は難関大学(上位国立、早慶、理科大)の志望者向け。
数学1A
問題1「因数分解」
単元:「数と式」 難易度:「基礎」
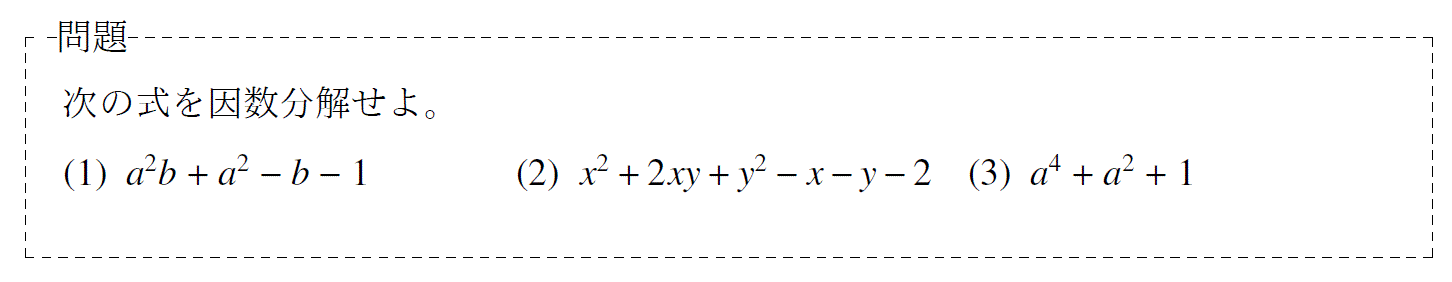
問題の解説プリント
(1)の動画解説 (2)の動画解説 (3)の動画解説
問題2「絶対値を含んだ不等式の問題」
単元:「数と式」 難易度:「基礎」

問題の解説プリント
「場合分けを使った解法」の動画解説 「グラフを使った解法」の動画解説 「同値変形を使った解法」の動画解説
問題3「2次の係数が文字を含んだ2次方程式の問題」
単元:「2次関数」 難易度:「基礎」

問題の解説プリント
動画による解説
問題4「6の倍数であることの証明問題」
単元:「整数」 難易度:「基礎」
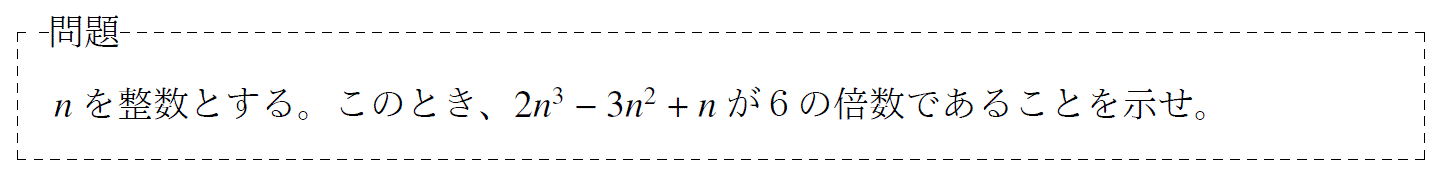
問題の解説プリント
動画による解説
問題5「方程式の整数問題について」
単元:「整数」 難易度:「基礎」
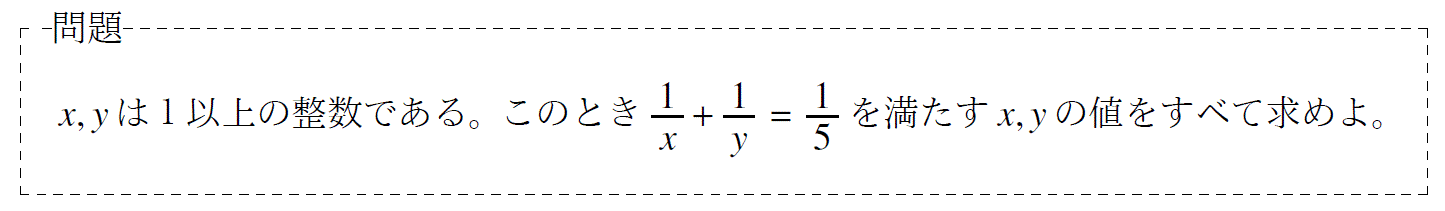
問題の解説プリント
問題6「方程式が有理数解をもつときの問題」
単元:「整数」 難易度:「発展」

問題の解説プリント
問題7「|A|=|B|の絶対値を含んだ方程式の解法」
単元:「数と式」 難易度:「基礎」
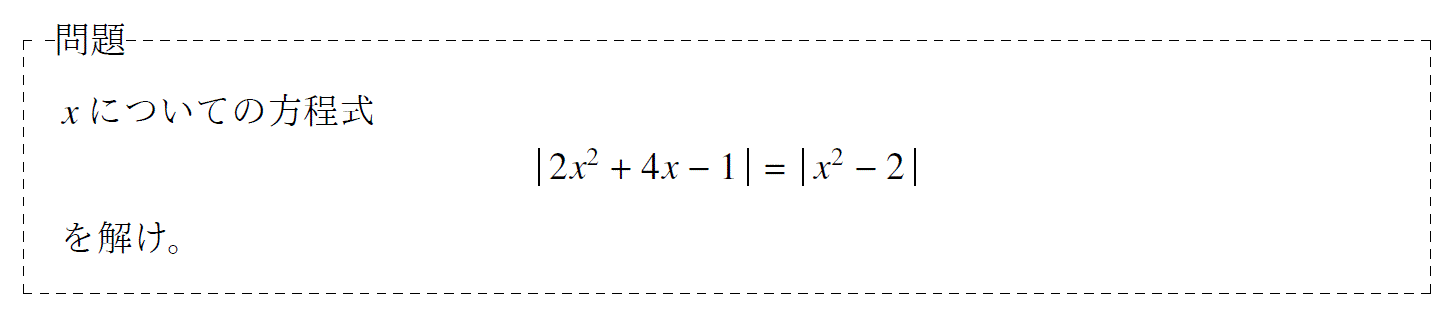
問題の解説プリント
問題8「一橋大学の整数問題の過去問」
単元:「整数」 難易度:「発展」
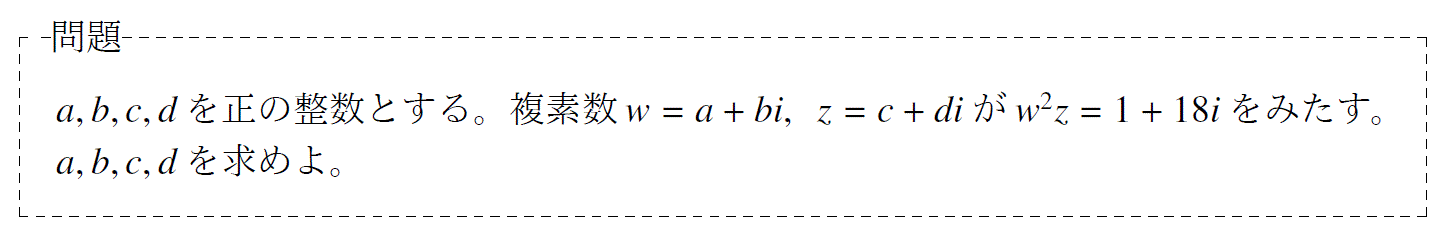
問題の解説プリント
問題9「新潟大学の過去問で反復試行の確率の問題」
単元:「確率」 難易度:「標準」

問題の解説プリント
問題10「岩手大学の過去問で2次関数の問題」
単元:「2次関数」 難易度:「基礎」

問題の解説プリント
問題11「不等式の定数に関する問題」
単元:「数と式」 難易度:「基礎」

問題の解説プリント
ユーチューブを使った動画解説
問題12「a+b+c=(一定)の文字消去について」
単元:「数と式」 難易度:「基礎」
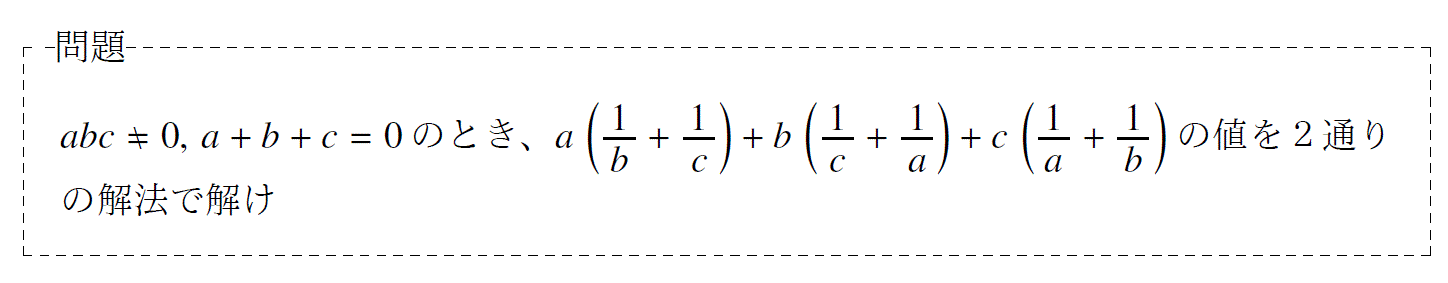
問題の解説プリント
問題13「グラフの共有点の個数の問題」
単元:「2次関数」 難易度:「標準」

問題の解説プリント
問題14「お茶の水女子大の整数問題の過去問」
単元:「整数問題」 難易度:「標準」

問題の解説プリント
問題15「グラフで示す2次方程式が実数解を持つ証明」
単元:「2次関数」 難易度:「基礎」
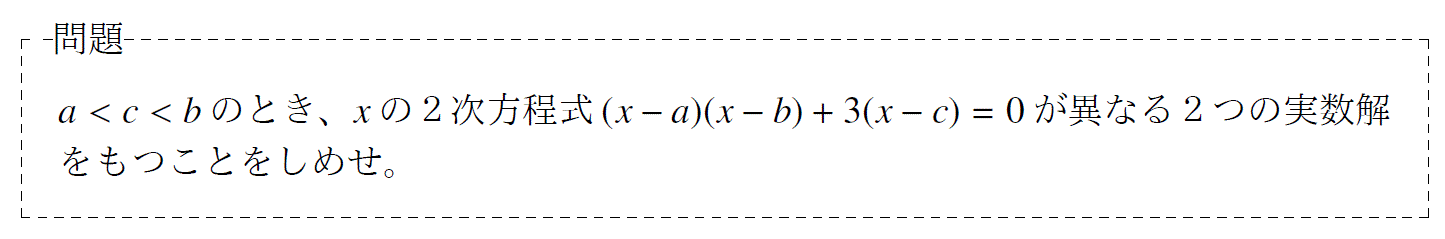
問題の解説プリント
問題16「連立方程式の同値変形」
単元:「数と式」 難易度:「発展」

問題の解説プリント
問題17「互いに素な整数の個数を求める問題」
単元:「整数」 難易度:「基礎」

問題の解説プリント
問題18「三角形の最大角の求め方」
単元:「三角比」 難易度:「基礎」
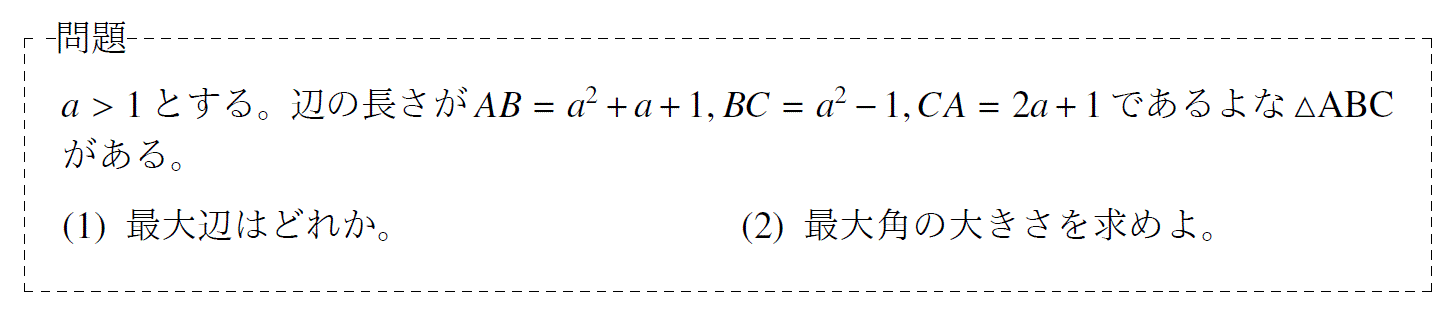
問題の解説プリント
問題19「確率の最大値の問題」
単元:「確率」 難易度:「標準」

問題の解説プリント
問題20「ガウス記号の解説」
単元:「数と式」 難易度:「基礎」

問題の解説プリント
問題21「背理法、対偶の証明」
単元:「数と式」 難易度:「基礎」

問題の解説プリント
問題22「確率の基本的な考え方」
単元:「確率」 難易度:「基礎」

問題の解説プリント
問題23「確率の問題を解説しました」
単元:「確率」 難易度:「基礎」

問題の解説プリント
問題24「一橋大学の整数問題を解説しました」
単元:「整数」 難易度:「標準」

問題の解説プリント
数学2B
問題1「虚数を係数にもつ2次方程式」
単元:「複素数と方程式」 難易度:「標準」

問題の解説プリント
動画による解説その1 動画による解説その2
問題2「解の配置を解と係数の関係で解く問題」
単元:「複素数と方程式」 難易度:「基礎」

問題3「置き換えの必要な三角関数の最大値・最小値問題」
単元:「三角関数」 難易度:「標準」

問題の解説プリント
動画による解説
問題4「x,y,zのうち少なくともひとつは1であることを示す証明問題」
単元:「式と証明」 難易度:「基礎」

問題の解説プリント
動画による解説
問題5「誘導付きの漸化式の問題について」
単元:「数列」 難易度:「標準」

問題の解説プリント
問題6「領域の最大値・最小値問題」
単元:「数列」 難易度:「標準」

問題の解説プリント
問題7「領域の図示の大学受験の問題」
単元:「図形と方程式」 難易度:「標準」

問題の解説プリント
問題8「指数を含んだ基本的な方程式の解法」
単元:「指数」 難易度:「基礎」

問題の解説プリント
問題9「シュワルツの不等式の関する問題」
単元:「不等式の証明・数列」 難易度:「発展」

問題の解説プリント
問題10「三角関数の最大値・最小値問題」
単元:「三角関数」 難易度:「標準」

問題の解説プリント
問題11「東大(文系)の過去問で、数学的帰納法に関する問題」
単元:「数列」 難易度:「標準」

問題の解説プリント
問題12「三角関数の基本的な置換をする問題」
単元:「三角関数」 難易度:「基礎」

問題の解説プリント
問題13「微積分の極値の差に関する問題」
単元:「微積分」 難易度:「標準」

問題の解説プリント
問題14「北海道大学の分数関数の過去問」
単元:「分数関数」 難易度:「標準」
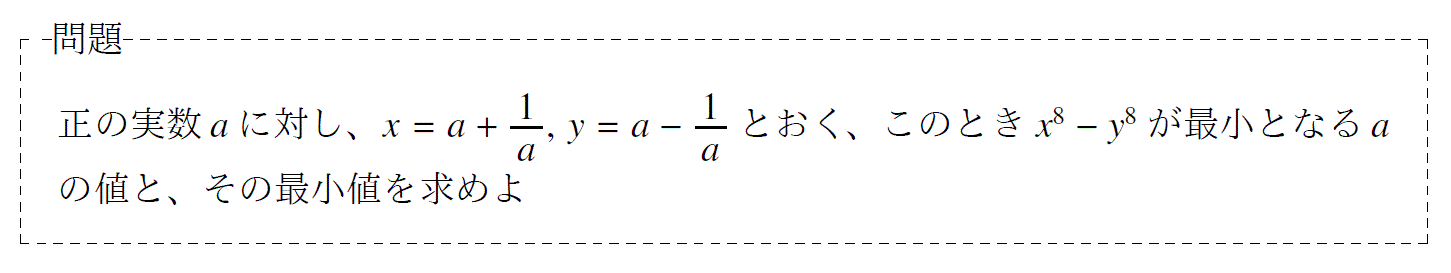
PDFファイルの解説プリント
問題15「三角関数の方程式の解説」
単元:「三角関数」 難易度:「基礎」

問題の解説プリント
問題16「誘導付きの漸化式の問題の解法」
単元:「数列」 難易度:「標準」

問題の解説プリント
問題17「直線のベクトル方程式について」
単元:「ベクトル」 難易度:「基礎」

問題の解説プリント
ユーチューブを使った動画解説
問題18「和歌山大学のベクトルの過去問」
単元:「ベクトル」 難易度:「標準」

問題の解説プリント
問題19「放物線と2接線によって囲まれる部分の面積」
単元:「微分積分」 難易度:「標準」

問題の解説プリント
問題20「数学的帰納法を使った証明問題」
単元:「数列」 難易度:「標準」

問題の解説プリント
問題21「東北大学の過去問で等式と不等式の証明」
単元:「式と証明」 難易度:「基礎」
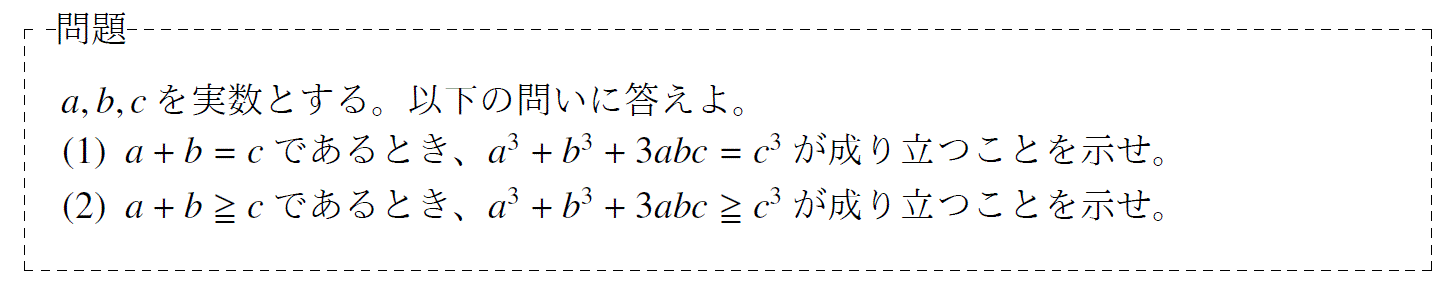
問題の解説プリント
問題22「ベクトルの内心の公式について」
単元:「ベクトル」 難易度:「基礎」
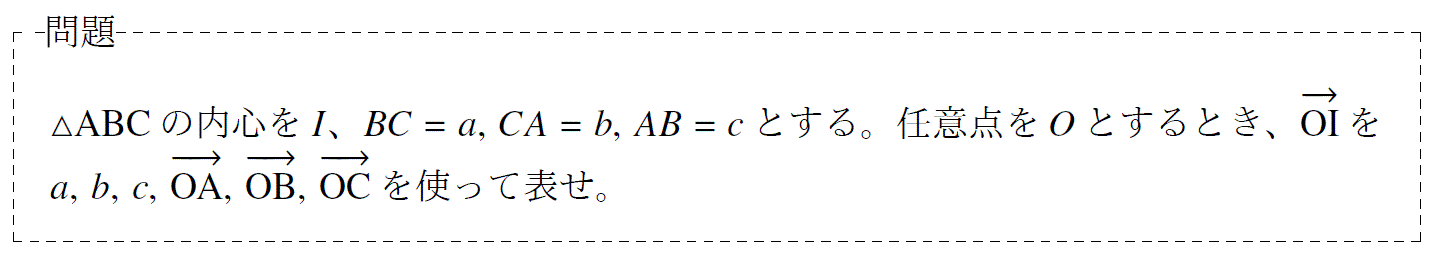
問題の解説プリント
問題23「図形でのベクトルの求め方」
単元:「ベクトル」 難易度:「基礎」

問題の解説プリント
問題24「漸化式の受験問題を解説しました」
単元:「数列」 難易度:「標準」

問題の解説プリント
数学3
問題1「簡単な定積分の問題」
単元:「定積分の計算」 難易度:「基礎」

問題2「定積分の本格的な入試問題」
単元:「定積分の計算」 難易度:「発展」

問題3「定積分を含んだ等式の微分」
単元:「定積分の計算」 難易度:「基礎」
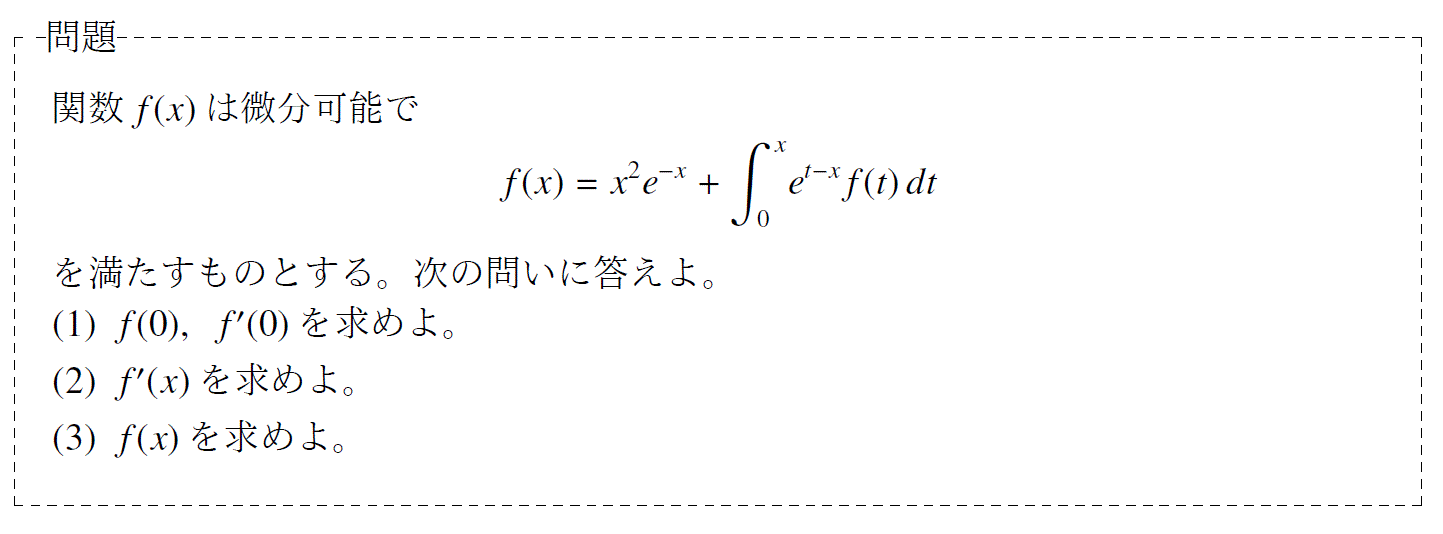
問題4「無限等比級数の解説プリント」
単元:「極限」 難易度:「基礎」

問題の解説プリント
動画による解説
問題5「無限等比級数の解説プリント」
単元:「積分」 難易度:「標準」

問題の解説プリント
問題6「関数の極限に関する問題」
単元:「極限」 難易度:「基礎」

問題の解説プリント
問題7「面積を使って示す不等式の証明問題」
単元:「積分」 難易度:「標準」
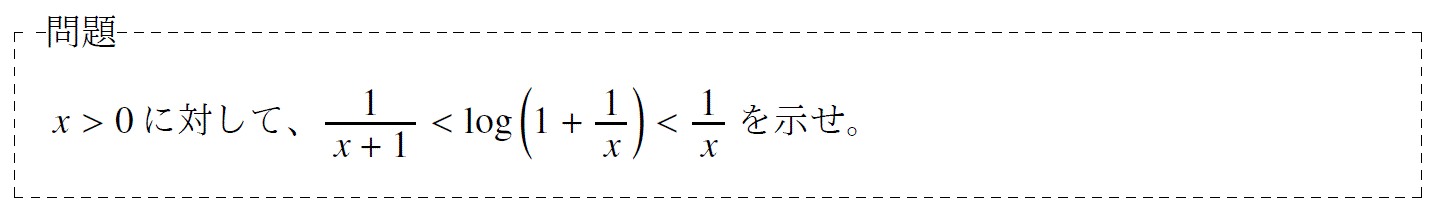
問題の解説プリント
問題8「平均値の定理を使って解く大小比較の問題」
単元:「微分」 難易度:「発展」

問題の解説プリント
問題9「お茶の水女子大学の過去問で、部分積分の問題」
単元:「積分」 難易度:「標準」

問題の解説プリント
問題10「筑波大学の過去問で、非回転体の体積の問題」
単元:「積分」 難易度:「標準」

問題の解説プリント
問題11「積分漸化式に関する問題」
単元:「積分」 難易度:「発展」

問題の解説プリント
問題12「区分求積法について」
単元:「積分」 難易度:「基礎」

問題の解説プリント
問題13「お茶の水女子大学の理系の微積分の問題」
単元:「微積分」 難易度:「発展」

問題の解説プリント
問題14「新潟大学の凸性を使った不等式の証明問題」
単元:「微積分」 難易度:「標準」

問題の解説プリント
問題15「北大の微積分の過去問の解説」
単元:「微積分」 難易度:「発展」

問題の解説プリント
問題16「筑波大学の微積分の過去問の解説」
単元:「微積分」 難易度:「標準」

問題の解説プリント
問題17「積分漸化式の本格的な大学受験の問題」
単元:「極限・積分」 難易度:「発展」

問題の解説プリント
ユーチューブを使った動画解説
問題18「筑波大学の積分の過去問」
単元:「積分」 難易度:「標準」
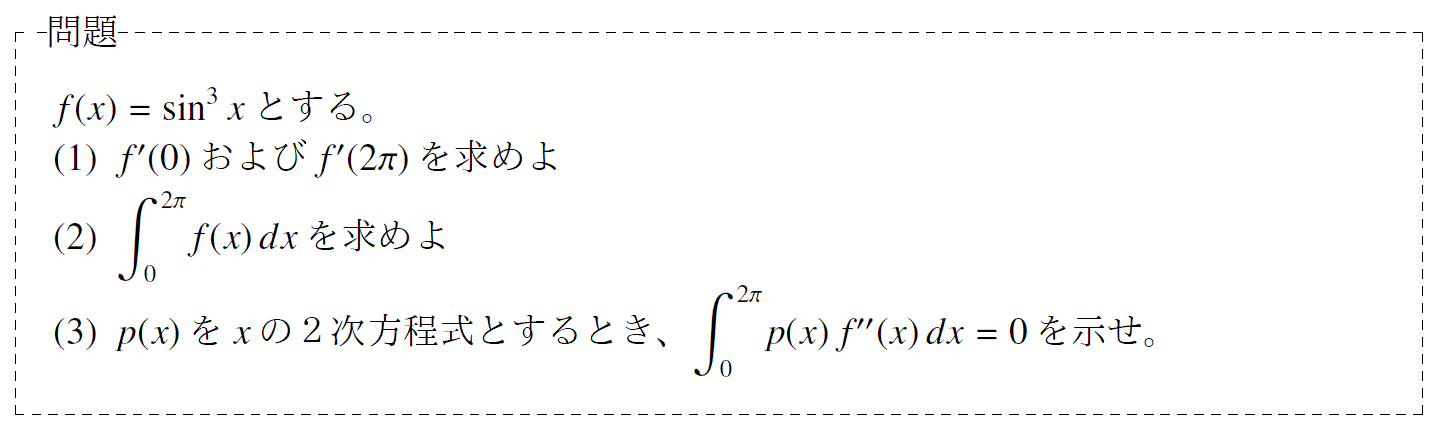
問題の解説プリント
問題19「筑波大学の楕円の接線と軌跡の過去問」
単元:「いろいろな曲線」 難易度:「標準」

問題の解説プリント
問題20「微分の最大値・最小値問題」
単元:「微分」 難易度:「基礎」

問題の解説プリント
問題21「複素数平面の本格的な受験問題」
単元:「複素数平面」 難易度:「発展」

問題の解説プリント
問題22「積分の入試問題」
単元:「微分積分」 難易度:「標準」

問題の解説プリント
問題23「お茶の水女子大学の積分の問題」
単元:「積分」 難易度:「標準」

問題の解説プリント
問題24「微分係数の定義に関する問題」
単元:「極限・微分」 難易度:「基礎」

問題の解説プリント
数学3の極限のプリントを無料でプレゼントします
数学3の極限の無料プリントを作りました。全部51問186ページの大作です。
このプリントをするだけで、学校の定期試験で満点を取ることができます。完全無料、もちろん売り込みもしません。読まないと損ですよ。
以下の緑のボタンをクリックしてください。
3年間大手予備校に行ってもセンターすら6割ほどの浪人生が、4浪目に入会。そして、入会わずか9か月後に島根大学医学部医学科合格!
数学の成績が限りなく下位の高校生が、現役で筑波大学理工学群合格!
教科書の問題は解けるけど、難しくなるとどう考えてよいのか分からない人が、東北大学歯学部合格!
その秘訣は、プリントを読んでもらえば分かります。
以下の緑のボタンをクリックしてください。

