ルールを覚えれば誰でもできる！あなたの数学偏差値を７０にするプリント！！

「なぜか解けてしまう。なんで、こんなに簡単に解けるんだろう。今まで苦労していたのは、なんだったのかな？」

これが、僕の授業を受けた生徒さんからよく受ける感想です。

でも、これって僕が何も特別なことをした訳ではないんです。数学って、覚えておかないといけないルールがあります（このときは、こうするといったものです）。それを覚えずに解こうとしても無理なんです。

「ルールを覚えたら解ける」っ言われても想像がつかないと思います。そこで、数列の漸化式の問題を解説してみます。以下の漸化式、国立大学では頻出です。ですが、進学校に通っている人でも解けない人が多いです。

パソコンやスマホで読んでいらっしゃる人が多いです。画面上では、数式をきれいに表記できないので、少し読みにくいかもしれません。ですが、僕の数学の問題へのアプローチの仕方が分かると思います。ぜひとも、読んでください。

問題　\(\large{a_1=1,\,\,\,\frac{a_{n+1}}{n}=\frac{a_{n}}{n+2}}\,\,\,\)の一般項を求めよ。

なんだかあっさり解けてしまったよね。今回は説明しやすいように簡単な問題を選びました。ですが、他の問題でもいっしょですよ。

「このときは、こうする」というルールを覚えていけば、自然とできるようになります。難しく感じる必要はないですよ。だって、上記の問題も「すごい難しい」なんていう人もいるけど、解法を読んで見たら簡単だったよね。

数学って、この程度なんです。プリントを使って高校生から、以下のような感想をいただきました。

数学って「こうきたらこうする」とか「このときはこうする可能性が高い」とか「これは、覚えるしか対処しようがないな」なんてものがあります。

そして、それらを覚えていけば、知らないうちに問題が解けるようになります。もちろん、難問も出題されます。そのときは、その場で考えないといけません。

ですが、実際の大学受験ではそこまで難しい問題が出題されることは少ないです。また、大学受験では満点は必用ありません。６，７割取れたら合格できます。だから、今回紹介しているプリントの問題ができるようになれば、ほぼすべての大学に合格することができます。

プリントは、簡単ではありません。大変です。それでも、これまで「数学を頑張りたい。でも、頑張り方が分からない」とか「勉強してもしてもできるようにならない」と困り切っている人に授業をして、そして結果を残しています。

このプリントは、それだけ挑戦しがいのあるものです。もし、心の底から数学の成績を上げたいのでしたら、このプリントで頑張ってください。

プリントの中身について

極限その１（数列の極限）　全５１問１９３ページ

極限その２（無限級数、無限等比級数について）　全１７問８０ページ

極限その３（関数の極限と極限の入試問題）　全２８問１５１ページ

微分（全範囲）　全１０５問５２１ページ

積分計算（不定積分と定積分の計算問題）　全８６問２３３ページ

積分の入試問題セクション１（不定積分・定積分に関する入試問題）　全２９問１９１ページ

積分の入試問題セクション２（面積に関する問題）　全３７問３１９ページ

積分の入試問題セクション３（体積に関する問題）　全２１問１５６ページ

積分の入試問題セクション４（区分求積法）　全１１問３５ページ

積分の入試問題セクション５（曲線の長さに関する問題）全４問１２ページ

積分の入試問題セクション６（媒介変数表示に関する問題）　全１１問９３ページ　

積分の入試問題セクション７（積分の不等式に関する問題）　全２５問１５８ページ

各プリントの内容

極限その１（数列の極限）　全５１問１９３ページ

数列の極限をまったくの基礎から解説しました。不定形、分数形の極限、\(r^n\)の収束条件・・・すべて解説

数列の漸化式では数学Ｂの数列の知識が必須です。理解できていない人が多い漸化式をすべて解説。これさえできれば漸化式は完璧です。

受験で、最頻出の\(|a_{n+1}-\beta|\leq\alpha|a_n-\beta|\)を示した後の、数列\(\{a_n\}\)の極限値を求める問題を３問掲載。他にも受験問題を多数掲載！

極限その２（無限級数、無限等比級数について）　全１７問８０ページ

\((1-1)+(1-1)+(1-1)+\cdots\)の無限級数は０に収束するが、\(1-1+1-1+\cdots\)の無限級数は収束しない理由は？

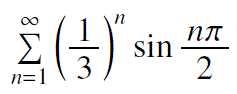なんていう、問題の解き方は？他にも受験問題を多数掲載！

極限その３（関数の極限と極限の入試問題）　全２８問１５１ページ

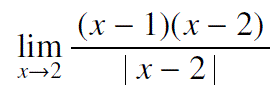が収束しない理由とは？

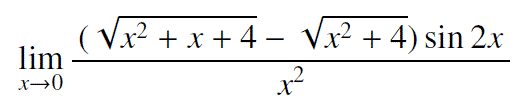といった複雑な極限値もルールに従えば単純に解けてしまいます。

数列の知識も必須です。多くの人が苦手にしている、格子点、群数列に関して基本から解説しています。

微分（全範囲）　全１０５問５２１ページ

微分をまったくの基礎から、受験レベルまで完全解説！

みんなが苦手としている２階微分、漸近線の求め方などグラフを徹底解説！

\(f'(x)\)の正負を知るにはグラフを使う方法がある。これさえ知っていれば、\(f'(x)=1+\frac{1-x}{\sqrt{2x-x^2}}\)といった複雑でも、\(f'(x)\)の正負を簡単に知ることができます。

積分計算（不定積分と定積分の計算問題）　全８６問２３３ページ

面積や積分に進む前に不定積分・定積分の計算を完璧に仕上げてもらいます。これができなければ理系の入試は厳しいです。難しく感じている人も多いですが、ごくごく簡単。単純に覚えていってもらえばいいだけです。置換積分、部分積分、部分分数分解を使った積分など、このプリントだけで積分計算は完璧です。

積分の入試問題セクション１（不定積分・定積分に関する入試問題）　全２９問１９１ページ

受験に最頻出です。にもかかわらず理解できていない人が多い！その問題を徹底解説！

「積分漸化式の最初の式変形は？」これを知らなければ、プリントをする価値があります。

このセクションは難しいです。その変わり変形するのが難しく同じ問題が繰り返し、繰り返し受験で出題されます。

島根大学医学科を合格した生徒さんです。大学の過去問をみると、この単元から１問でそう、だから、この単元だけは絶対に完璧に解けるようになるまで繰り返し頑張ってもらいました。

そして、出題されたのがこのプリントの問題１９に掲載している問題とまったく同じ問題が出題されました。「解けました！」と喜んでいたんですけど、「まったく同じ問題なんだから解けないと困ります」。難しいけど、ひねりようがない単元です。このプリントを繰り返し解けば、入試レベルまで完璧です。

積分の入試問題セクション２（面積に関する問題）　全３７問３１９ページ

なぜ、積分で面積が求まるの？これが分かれば、側面積など複雑な面積も意味を考えて簡単に面積を求められるようになります。

受験では頻出だが、多くの人が苦手にしている逆関数の面積に関する問題を掲載！

面積だけでなく大学受験の総合問題も掲載！媒介変数の軌跡はなぜ媒介変数を消去したら求められるの？直線のベクトル方程式、回転移動、など受験生が苦手としている部分を徹底解説！

積分の入試問題セクション３（体積に関する問題）　全２１問１５６ページ

体積の意味を解説。\(\int{}{}\pi y^2\,dx\)の意味を解説。これが分かれば、\(x\)軸回転や\(y\)軸回転以外、例えば直線\(y=1\)の周りに回転する、といった問題も簡単に解けます。

受験では必須の知識、斜回転体の積分、バウムクーヘン型の積分、パップスギュルダンの定理等、高校ではあまり教わらないテクニックを多数解説！

非回転体の体積、空間座標の回転体の体積といった難関大学では頻出だが、多くの参考書や問題集では、「こんなのもありますよ」程度にしか解説されていない問題を徹底解説！

積分の入試問題セクション４（区分求積法）　全１１問３５ページ

意味も分からずに解いている人が多い、区分求積の意味を解説。

区分求積法は、大問で出題されることは少ないです。ですが、出題されるとしたら以下のような問題です。
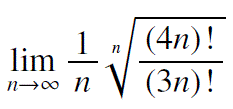過去、北大、東工大、金沢大、防衛医科などほぼ同じ問題が繰り返し、繰り返し出題されています。

積分の入試問題セクション５（曲線の長さに関する問題）全４問１２ページ

曲線の長さは定積分の計算がややこしいです。でも、考え方にコツがあります。\(\int_{}{}\sqrt{1-\sin x}\,dx\)の積分ができない人は注意してください。

積分の入試問題セクション６（媒介変数表示に関する問題）　全１１問９３ページ

入試では頻出だが、多くの高校生が苦手にしている媒介変数表示を徹底解説！

リサージュ曲線、サイクロイド、内（外）サイクロイド（円をころがる軌跡です）、アステロイドなど有名曲線はすべて網羅。もちろん、すべて丁寧な解説付きで、しっかりと理解できます。

\((x,y)=(r(\theta)\cos\theta,r(\theta)\sin\theta)\)の形で表される曲線の面積は、おうぎ形の面積を足し合わせて求めることができます。このような受験テクニック的な問題も徹底解説！

積分の入試問題セクション７（積分の不等式に関する問題）　全２５問１５８ページ

受験で頻出の、不等式の積分の問題を解説！

面積を使った大小比較、単調な関数を使った不等式のつくり方他、多くの学校ではテキトウにしか扱わない箇所を丁寧に解説しています。

プリントをすれば上記の知識がすべて手に入ります。スゴくないですか？

「なぜ、ここでこのように変形したのか？」ということを徹底的に解説しています。ですから、数学があまり得意でない人でもプリントを読み込むことで、自然と理解できるようになってきます。

上記のプリントが完璧にできたら、ほぼすべての大学に合格できますよ。最難関と言われる国立医学部医学科にも多くの人が合格していっています。

と言って、内容が難しすぎることはありません。まったく、「数学ができない」というのでしたら難しいかもしれません。ですが、それ以外の人でしたら大丈夫ですよ。「数学なんて見るのもイヤ」と拒絶するほど数学が苦手な人以外は大丈夫です。

プリントの料金について

プリントの料金は、上記のプリントすべてがセットで税込み３９，８００円です。

まずはサンプルから

ここまで、僕がプリントのメリットばかりを話してきました。

ですが、こんなネットの話し信用できないですよね。僕が、あなたの立場だったら「プリントやってみたい気もするけど、なんだか怪しいしやめておこう・・・」と思うでしょう。きっとあなたもその不安があると思います。

いきなり数万円もする教材を買うのは気が引けますよね。そこで、サンプルとして「数列の極限」のプリントを無料で提供いたします。

このプリントは一切無料です。プリントを試してみて「これならいけそう！他の単元のプリントも欲しい！」となりましたらメールで連絡してください。

プリントをやってみた上で「あわないな」と感じたら無視してください。金額は一切発生しないので安心してください。

納品形式

ＰＤＦファイルです。

お申込み後、銀行振り込みにてプリントの料金をお支払いしてもらいます。

入金確認後、メールにてダウンロード先のＵＲＬをお知らせします。それをクリックしていただいたらすぐにご覧になれます。

「数列の極限」のサンプルを試してみる

以下より、サンプルの申請をしてください。「お試しより全部のプリントが欲しい！」という方もいらっしゃいます。以下のフォームでどちらかを選択してください。

QandA　あなたの質問に答えます。

Q.プリントは、プリントアウトすることができますか？

A.可能です。各自、ご自宅でプリントアウトしてお使いください。

Q.スマホでもプリントを見ることはできますか？

A.閲覧自体は可能です（iPhoneなら問題なく見ることができます。アンドロイドの場合、PDFファイルを見るために、無料のアプリが必要なことがあります）。ただ、スマホの場合、モニターが小さいので見にくいかもしれません。スマホに慣れている人であれば問題ないかもしれません。

Q.分からないところが出てきた場合、質問に答えてくれますか？

A.メールで質問をしてもらえば、できる限り回答します。できる限りと言ったのは、あまりにもくだらない質問(お気軽に聞いてもらった大丈夫ですよ。ただ、\(\sin60^{\circ}\)っていくらですか？なんて、簡単すぎるものは自分で調べてください)や何度も質問をしすぎる（少しは自分で考えないとできるようになりません）などそういったときはお答えしかねます。

繰り返しになりますけど、気軽に質問をしてくださいね。ただ、あまりにも度を超えて、生徒さん本人のためにならないと考えたら、お答えしかねる場合もあるってことです。

僕の目標は、「あなたに数学の成績をあげて、志望校に合格すること」ただ、それだけです。これにつながりそうなことだったら喜んで行動します。ですが、そうでない場合、対応いたしかねます。

Q.プリントのページ数が多すぎます。それほど多くの量をこなせるか不安になります。

A.プリント、たしかにページ数が多いですよね。量が多すぎる！なんてついつ思ってしまいます。

プリントを作った僕でも、「ページ数が多すぎる！！」なんて思います。でも、問題数じたいは他の問題集とそれほど変わらないんです。少し多めといった程度です。

他の問題集の４，５倍のページ数はあります。それは何か？と言えば丁寧に説明しているからなんです。

大雑把な地図を渡されて「目的地に行ってください」と言われても、目的地にたどりつきません。そんな人でも、詳細な地図が渡されたら目的地にたどりつくことができます。

僕のプリントは、詳細な地図のようなものです。大雑把な地図を渡されて「ああでもない、こうでもない」とさまよっていてもいくら頑張っても目的地にたどりつきません。

だから、多少（といいますか、かなり）ページ数は多いです。でも、読み進めていけば「ああ、数学ってこういうふうに考えるのか」ということが、どんどん自分の身に入ってきます。

そうすると、これまで考えられないほどの成績アップにつながりますよ。３年間、大手の予備校に通い続けてまったくできなかった人が、わずか８か月ほどで国立大学医学部医学科に合格しました。その人は、「数学が得意でない！」と言っていました。でも、そうじゃないんですよね。

もともと、実力はあったんです。ただ、勉強の仕方を間違っていただけなんですよね。だから、あなたも頑張れて、きっと志望校に合格しますよ。

Q.どうしても１対１で解説をして欲しい

A.コチラですと、毎週１回60分。月々20,000円で１対１の授業を行っています。現在のところ、この授業をお申込みされた方は無料でプリントを見ることができます。

Q.プリントだけで４万円近くって高くないですか？

A.本当は、あまり金額の話ししたくないんですよね。僕、このプリントを作るのに、相当の時間がかかりました。製作に１年半以上かかったんです。自分で勝手に作っているので当然、無報酬です。

それまでは、毎日朝から晩まで毎日１０時間以上授業をしてきました。でも、時間的な制約もあり、もっとこうしたい、と思っても授業時間で解説をしきれないこともあったんです。

だから、一人で勉強できるプリントをどうしても作りたかったんです。「このプリントを使えば、ひとりで勉強できる。僕が、すべて解説できなくても勉強できる」と、一人でコツコツと少なくとも１，０００時間以上の時間をかけてプリントを作りました。

プリントは、４万円近くして確かに高額です。ですが、私立大学を１校受験したらそのくらいします。だから、コスパ的に完全にお得です。

先ほどあげた、医学部に合格した人の話です。医学部の場合、数千万円の養成費が必要だそうです。彼は、国立に受かったので数千万円の価値を手にしました（この考えはいかがなものかもしれませんが、単なる例えです）。そうすると、このプリントの数万円なんて非常に安いものです。

何を言いたいのかと言うと、「一生懸命頑張って欲しい！」ということなんです。僕は純粋に、「数学のせいで大学に行けない、夢をあきらめなければいけない」そういう人の手助けをしたいだけです。

本音をいいます。たった、３９，８００円です。高校生は無理かもしれませんが、卒業していたらアルバイトでも簡単に稼げる金額です。もし、本気で大学にいきたいのなら、決して高くありません。むしろ格安です。

とにかく一生懸命このプリントに立ち向かってくれる人のみを募集しています。一生懸命勉強をすれば、それだけ、価値のあるものです。

熱くなってしまって申し訳ありません。僕の気持ちは唯一「このプリントで一生懸命頑張って欲しい」ただ、それだけなんです。

だから、ホントはただでもいい（でも、それじゃあ僕も生活があるから困るかな？（笑顔））。そんな気持ちです。

お金の話しって難しいですよね。「安すぎますよ。少なくとも、この１０倍くらいの価値があります」という人もいれば、「高すぎるよ」という人もいます。

でも、これだけは言いたいです。「頑張れば、頑張るだけこのプリントには価値があります」ということを。だから、本気で頑張りたい、という人だけに購入していただきたいです。

Q.学習塾の経営者です。塾で、河見さんのプリントを使いたいのですが、どうしたらいいですか？

A.このプリント、いくつかの塾・予備校でも使っていただいております。個人で申し込んで勝手に学習塾で使われることはお控えください。

個別に相談します。こちらのフォームより、お問合せください。

生徒様の声

プリントの購入を希望される方は以下の緑のボタンより注文フォームにお進みください。